超松弛迭代法两个函数对比

综合讨论区 性能优化
1 
using BenchmarkTools, LinearAlgebra, Traceur

function sor(A,b,X,mn,w,ww)
    # sor - Description
    #
    # Syntax: output = myFun(input)
    #
    # mn = 最大迭代次数
    # w = 误差精度
    # ww = 松弛因子
        it = 1                             # 迭代次数初值
        D = Diagonal(A)
        L = LowerTriangular(-A)+D
        U = UpperTriangular(-A)+D
        M = inv(D-ww*L)*((1-ww)*D+ww*U)    # 迭代矩阵
        g = ww*inv(D-ww*L)*b               # 迭代格式中的常数项
        while it <= mn
            x = M*X+g
            if norm(x-X,Inf) < w
                # disp('迭代次数为')
                # in
                return it,x
            end
            X = x
            it += 1
        end
        println("最大迭代次数内不收敛！")
end

A = Array(fill(1, 4,4))
[A[i,i] = -4 for i in 1:4]
b = [1;1;1;1]
mn = 1e5
w = 1e-5
ww = 1.1
x = zeros(4, 1)
XX = zeros(4, 1)
it,x = sor(A,b,XX,mn,w,ww)

精确解是[1;1;1;1]
迭代17次后的数值解为：
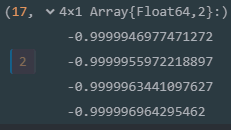
image
但是运行时间比较慢，并且有内存分配
8.249 μs (98 allocations: 10.25 KiB)

采用inplace进行优化

function sor!(A,b,x,X,mn,w,ww)

    # mn = 最大迭代次数
    # w = 误差精度
    # ww = 松弛因子
        it = 1                             # 迭代次数初值
        D = Diagonal(A)
        L = LowerTriangular(-A)+D
        U = UpperTriangular(-A)+D
        M = inv(D-ww*L)*((1-ww)*D+ww*U)    # 迭代矩阵
        g = ww*inv(D-ww*L)*b               # 迭代格式中的常数项
        while it <= mn
            x[1:end] = M*X+g
            if norm(x-X,Inf) < w
                # disp('迭代次数为')
                # in
                return nothing
            end
            X = x
            it += 1
        end
        println("最大迭代次数内不收敛！")
end
A = Array(fill(1, 4,4))
[A[i,i] = -4 for i in 1:4]
b = [1;1;1;1]
mn = 1e5
w = 1e-5
ww = 1.1
x = zeros(4, 1)
XX = zeros(4, 1)
sor!(A, b, x, XX, mn, w, ww)

迭代2次就不迭代了，解也不精确
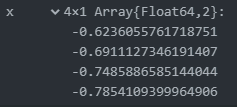
image
不知道为什么不往后迭代了
求建议

2

binding 问题？

3

怀疑的原因：
当A作为外部共享方式传入时，构造的D、L与U均共享了同一个内存区

4

根据您的指导，修改了下代码

using BenchmarkTools, LinearAlgebra
function sor!(A,b,x,X,mn,w,ww)

# mn = 最大迭代次数
# w = 误差精度
# ww = 松弛因子
    it = 1                             # 迭代次数初值
    D = Diagonal(A)
    L = LowerTriangular(-A)+D
    U = UpperTriangular(-A)+D
    M = inv(D-ww*L)*((1-ww)*D+ww*U)    # 迭代矩阵
    g = ww*inv(D-ww*L)*b               # 迭代格式中的常数项
    while it <= mn
        x[:] = M*X+g
        if norm(x-X,Inf) < w
            # disp('迭代次数为')
            # in
            return nothing
        end
        X[:] = x[:]
        it += 1
    end
    println("最大迭代次数内不收敛！")

end
A = Array(fill(1, 4,4))
[A[i,i] = -4 for i in 1:4]
b = [1;1;1;1]
mn = 1e5
w = 1e-5
ww = 1.1
x = zeros(4, 1)
XX = zeros(4, 1)
@btime sor!(A, b, x, XX, mn, w, ww)
3.307 μs (49 allocations: 4.97 KiB)
用@trace 查看的话，会出现非常多的警告

image
image710×403 5.13 KB

原来的sor函数运行时间：

8.249 μs (98 allocations: 10.25 KiB)

您帮忙看看，还有优化空间没？谢谢您！

5

谢谢，修改了下，迭代运算结果没问题了