msh.jl如下:
module msh
using PyPlot
export plotMesh
struct Mesh
coords
function Mesh(n1,n2)
@assert (n1 > 0 && n2 > 0) "Mesh arguments must be positive"
coords = createCoords(n1,n2)
new(coords)
end
end
function createCoords(n1,n2)
#Fill coords array
coords = zeros(2,n1n2);
cnt = 1
for i = 1:n2
for j = 1:n1
coords[1:2,cnt] = [j-1,i-1]
cnt = cnt+1
end
end
r = 1.0/(4n1)*rand(size(coords)[1], size(coords)[2])
coords = coords + r #“random” pertubation of grid
return coords
end
function plotMesh(m::Mesh,c::String)
#Plot coordinates
for i = 1:size(m.coords)[2]
plot(m.coords[1,i],m.coords[2,i],marker="o",color =c, markersize = 10)
end
end
end
代码如下:
include(“msh.jl”)
using PyPlot
using DifferentialEquations
using LinearAlgebra
###########################################################################################
INPUT
###########################################################################################
n = 10 #number of particles will be nn
N = nn
#set up mesh
m = msh.Mesh(n,n)
npull = n #number of elements being pulled at a constant speed
nhold = n #number of elements being held at their initial position
#Set time interval [0,maxT]
maxT = 4
#Set up matrix of spring constants
global K
K = zeros(N,N)
for i = 1:N
for j = i+1:N
K[i,j] = 2^(-norm(m.coords[:,i] - m.coords[:,j],2)+1) #compute 2-norm because why not
K[j,i] = K[i,j]
end
end
#strengthen bond to the boundary nodes
for i = 1:nhold
K[i,:] *= 10
K[:,i] *= 10
end
for i = N-npull+1:N
K[i,:] *= 10
K[:,i] *= 10
end
##################################################################################################
#count the number of bonds each element has
global nbonds = Dict{Float64, Array{Float64,2}}()
nbonds[0.] = N*ones(N,1)
c1 = [4 2] #choose speed in x and y direction
function f(x,p,t)
global K
H = ones(size(K))
xh = [m.coords[1,1:nhold] m.coords[2,1:nhold];
hcat(x[1:N-npull-nhold], x[N-npull-nhold+1:2*(N-npull-nhold)]);
(c1[1]tones(size(m.coords[1,N-npull+1:N]))+m.coords[1,N-npull+1:N]) (c1[2]tones(size(m.coords[2,N-npull+1:N]))+m.coords[2,N-npull+1:N])]’
for i = 1:N
for j = i+1:N
if norm(xh[:,i]-xh[:,j]) > 10
H[i,j] = H[j,i] = 0
end
#make particles repulse each other/try to enforce order
#confuses the ode solver for some reason
#if norm(xh[:,i] - xh[:,j]) < 0.1 && H[i,j] > 0
# H[i,j] = -H[i,j]
# H[j,i] = H[i,j]
#end
end
end
K = K.*H
#recalculate the number of bonds
global nbonds
nbonds[t] = sum(K.!=0, dims=2)
#Create stiffness matrix
A = zeros(N-npull-nhold,N-npull-nhold)
for i = 1:N-npull-nhold
A[i,i] = -sum(K[i+nhold,1:N]) #diagonal is special ![]()
for j = 1:N-npull-nhold
if(i!=j) A[i,j] = K[i+nhold,j+nhold] end
end
end
#Create “forcing” term
B = zeros(2*(N-npull-nhold),1)
for i = 1:N-npull-nhold
B[i] = sum((c1[1]tones(size(m.coords[1,N-npull+1:N])) + m.coords[1,N-npull+1:N]).K[i+nhold,N-npull+1:N]) + sum(K[i+nhold, 1:nhold].m.coords[1,1:nhold])
B[i+N-npull-nhold] = sum((c1[2]tones(size(m.coords[2,N-npull+1:N])) + m.coords[2,N-npull+1:N]).K[i+nhold,N-npull+1:N]) + sum(K[i+nhold, 1:nhold].m.coords[2,1:nhold])
end
y = [Ax[1:N-npull-nhold]+B[1:N-npull-nhold];
Ax[N-npull-nhold+1:2(N-npull-nhold)]+B[N-npull-nhold+1:2(N-npull-nhold)]]‘’
return [x[2*(N-npull-nhold)+1:end]; y]
end
#Solve system of second order ODE using ode45
y0 = [m.coords[1,nhold+1:N-npull];
m.coords[2,nhold+1:N-npull];
zeros(2*(N-npull-nhold))] #initial conditions
#initial positions given by mesh, initial speed set to zero
#tout,yout = ode45(f, y0,[0:0.1:maxT;])
prob = ODEProblem(f, y0,(0.0,maxT))
#alg = Tsit5()
sol = solve(prob)
tout = sol.t
yout = sol.u
ys = hcat(yout…)’
print("Number of timesteps: ", size(tout)[1], “\n”)
#Plot position of particles at time step
cnt = 1
minh = minimum(tout[2:end] - tout[1:end-1])
differ = maximum(tout[2:end] - tout[1:end-1])/minh
if differ > 5 i_step = Integer(floor(differ/5)) end
for tstep = 1:i_step:Integer((size(tout)[1]-1)) ##################################
global cnt
currenth = tout[tstep+1] - tout[tstep]
for j =1:i_step:Integer(ceil(currenth/minh))
broken_t = (nbonds[tout[tstep]] .< 50)[:,1]
yh = [m.coords[1,1:nhold] m.coords[2,1:nhold];
vcat(ys[tstep, 1:N-npull-nhold]‘, ys[tstep, N-npull-nhold+1:2*(N-npull-nhold)]’)';
(c1[1]*tout[tstep]*ones(size(m.coords[1,N-npull+1:N]))+m.coords[1,N-npull+1:N]) (c1[2]*tout[tstep]*ones(size(m.coords[2,N-npull+1:N]))+m.coords[2,N-npull+1:N])]
plot([-5,20],[-5,25], markersize = 0, linestyle = “None”) #sloppy way of setting axis sizes
plot(yh[ broken_t,1], yh[ broken_t,2], marker=“o”, markersize=10, color = “r”, linestyle = “None”)
plot(yh[.~broken_t,1], yh[.~broken_t,2], marker=“o”, markersize=10, color = “b”, linestyle = “None”)
savefig(string(“Plots/plot”, cnt))
clf()
cnt += 1
end
end
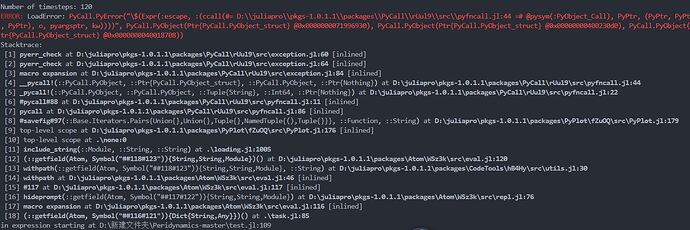
错误:
第109行代码:
for tstep = 1:i_step:Integer((size(tout)[1]-1))