其实不是这样的，这里的BitArray{1}应该跟上面的那位老兄说的一样，是用整数来表示，根据索引取其某一位。
julia> sizeof(trues(64)) == sizeof(trues(8))
true
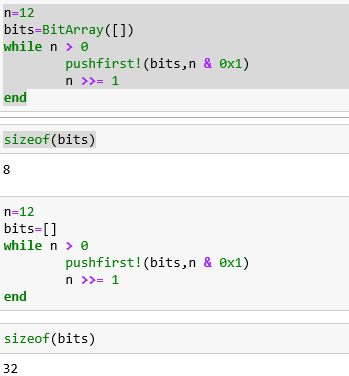
这是特殊的类型
function primesCount2(maxn::Int64)
mark_array = trues(maxn)
sqrt_maxn = floor(Int64, sqrt(maxn))
@inbounds for i = 3:2:sqrt_maxn
if mark_array[i]
@inbounds for j = i^2:2i:maxn
mark_array[j] = false
end
end
end
cnt = 1 # count for prime 2
@inbounds for i in 3:2:maxn
if mark_array[i]
cnt += 1
end
end; cnt
end
我也优化了一下，虽然还比你那个慢20+%，不过如果要给出所有素数，结果未必会这样。
522.937 ms (3 allocations: 11.92 MiB)
5761455
391.883 ms (3 allocations: 5.96 MiB)
5761455
[Finished in 28.0s]
你这一测试
nlen=cld(n, 2)
谢谢，不知道有这个函数
您这个确实很快，我试图做多种优化，也不能达到您这种速度。
这是matlab的库函数，我发起的项目，转写matlab库函数到julia
我想问一下您那里面多余的那个temp变量为什么不删除呢？
应该是测试着写着，没有注意，删掉就行
我把你的代码稍微修改了一下，省了将近一半内存。
function primes(maxn::Int64)
half = cld(maxn, 2)
p = trues(half)
for i = 3:2:isqrt(maxn)
if p[div(i + 1, 2)]
for j = div(i^2 + 1, 2):i:half
p[j] = false
end
end
end
p = (1:half)[p]
p .*= 2
p .-= 1
p[1] = 2
return p
end
方法一：常规方式
# Get last number of Fibonacci sequence with manual-written code
function fib(a::Int,b::Int,n::Int)
for i in 1:n
a,b=b,a+b
end
return b
end
@time x=fib(1,1,10^8)
#0.046809 seconds (1 allocation: 16 bytes)
方法二：Julia方式（面向接口的编成）- 参考官方Julia手册章节：接口
# Implement an iterator for Fibonacci sequence
mutable struct TwoElements{T}
a::T
b::T
end
struct Fib{T}
init::Tuple{T,T}
count::Int
f::TwoElements{T}
end
Fib(init::Tuple{T,T},count::Int) where T=Fib(init,count,TwoElements(init[1],init[2]))
Fib(first,second,count::Int)=Fib((first,second),count)
"""
Sequental iteration is implemented by the `iterate` functon.
Any object that defines this function is iterable and can be used in the `many functions that rely upon iteration`.
"""
Base.iterate(F::Fib,state=1) = state > F.count ? nothing : begin F.f.a,F.f.b=F.f.b,F.f.a+F.f.b; (F.f.b,state+1) end
"""
By extending the `eltype` and `length` method, we can do more about our iterable type!
"""
Base.length(F::Fib) = F.count
Base.eltype(::Type{Fib{T}}) where T = T
"""
By extend `getindex`, we can access the indexed element!
"""
function Base.getindex(F::Fib,i::Int)
1 <= i <= F.count || throw(BoundsError(F,i))
f = F.f.a
for value in Fib(F.f.a,F.f.b,i)
f=value
end
return f
end
"""
To support the syntax S[end], we must define `lastindex`, and also `firstindex` to specify the first valid index !
"""
Base.firstindex(F::Fib)=1
Base.lastindex(F::Fib)=F.count
#Get the last number of Fib sequence
@time y=Fib(1,1,10^8)[end]
#0.058757 seconds (1 allocation: 16 bytes)
#Get the whole Fib sequence
@time c=collect(Fib(1,1,10^8))
#0.513933 seconds (4 allocations: 762.940 MiB, 27.56% gc time)
解析函数法最快吧，设置两个初值，解差分方程算出通项公式。通过通项公式计算第n项，再取个整。应该比递推快。
