数学符号介绍
说到基础线性代数,我们还是从最基本的矩阵乘法开始吧。当然在那之前我们还是先定义一些基本数学符号的意义。虽然说用爱因斯坦求和约定十分的方便,但是在线性代数的设定下会造成一些误解。所以我们还是要明确地写出 \sum 求和符号。我们之后会用在数值分析里经典的Householder notation,即小写希腊字母为标量,小写拉丁字母为矢量,大写拉丁字母为矩阵。如 C \leftarrow \alpha A^\dagger B^\dagger + \beta C 是广义矩阵乘法 (gemm),其中 \dagger 代表共轭转置,即Julia的 ' 算符。值得注意的是,这个教程之后会基本上用 (\cdot)^\dagger 来代替 (\cdot)^T ,因为绝大多数情况下共轭转置在复数和实数的情况下都成立。
矩阵-向量乘法
首先矩阵-向量乘法的定义是 b_i = \sum_{j=1}^n A_{ij}x_j, ~~i=1,\cdots,m ,根据这个定义我们可以很容易的写出Julia的对应代码。
function matmul!(b::AbstractVector, A::AbstractMatrix, x::AbstractVector, fillzero=true)
fillzero && fill!(b, zero(eltype(b)))
m, n = size(A)
@assert n == length(x) && m == length(b)
@inbounds for j in 1:n, i in 1:m
b[i] += A[i, j]*x[j]
end
b
end
matmul(A::AbstractMatrix, x::AbstractVector) = matmul!(zeros(eltype(b), size(A, 1)), A, x, false)
using LinearAlgebra, Test
let
@testset "Matrix-Vector Product Tests" begin
A = rand(5,4); x = rand(4); b = rand(5)
d = A*x + b
matmul!(b, A, x, false)
@test A*x ≈ matmul(A, x)
@test d ≈ b
end
end
矩阵-矩阵乘法
矩阵-矩阵乘法的定义是 C_{ij} = \sum_{k=1}^pA_{ik}B_{kj} 。相对应的Julia代码就是
function matmul!(C::AbstractMatrix, A::AbstractMatrix, B::AbstractMatrix, fillzero=true)
fillzero && fill!(C, zero(eltype(C)))
m, p = size(A); n = size(B, 2)
@assert m == size(C, 1) && n == size(C, 2) && p == size(B, 1)
@inbounds for j in 1:n, k in 1:p, i in 1:m
C[i, j] += A[i, k]*B[k, j]
end
C
end
matmul(A::AbstractMatrix, B::AbstractMatrix) = matmul!(zeros(eltype(B), size(A, 1), size(B, 2)),
A, B, false)
using LinearAlgebra, Test
let
@testset "Matrix-Matrix Product Tests" begin
A = rand(5,4); B = rand(4, 7); C = rand(5, 7)
D = A*B + C
matmul!(C, A, B, false)
@test A*B ≈ matmul(A, B)
@test D ≈ C
end
end
从上面的例子很容易看出,计算结果和for循环的顺序无关。但是计算速度和for循环的顺序有关系吗?
julia> A, B, C = [rand(480, 480) for i in 1:3];
julia> using BenchmarkTools, Test
julia> @btime matmul!($C, $A, $B, false); #jki
23.273 ms (0 allocations: 0 bytes)
julia> @btime matmul2!($C, $A, $B, false); #kij 见脚注1
285.066 ms (0 allocations: 0 bytes)
julia> matmul2!(C, A, B, true); @test C ≈ A*B
Test Passed
可以看出,改变for循环的顺序会很大程度上的影响性能。如果想看各种for循环顺序的性能的话,可以看这个Jupyter Notebook。
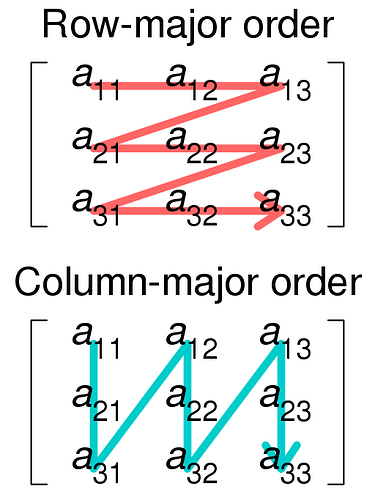
三个for循环里的表达式是 C[i, j] += A[i, k]*B[k, j]。你可能会问,我们能从这里直接看出for循环应该怎么摆放才能最快吗?当然是可以的。首先,要知道Julia和Fortran一样是column major的,即为向下在内存中行走是连续的,如图。而且还要知道比起CPU缓存来说,主内存的延迟很大,所以读取一块内存以后要尽量一直用。
最内层的循环应该使用 i,因为这样A[i, k]和C[i, j]在最内层循环内都是连续地读写内存。再上一层的循环应该用 k。因为这样的话,每完成一次对 i 的循环,电脑直接在B上读取下一个元素,而且不动 C。这个时候C的一竖列在CPU的快速缓存上,所以我们要留住C。相反,如果在第二层循环用j的话,这样既没有留住C也会在B矩阵上跳,所以不是好选择。这样最后一个循环就是要用j了。
一般来说,优化思路就是去 尽量减少内存移动 。这点在应用线性代数里十分的重要,以后几乎所有的优化都是为了减少内存移动。因为比起CPU的缓存,读写内存十分的慢。如果CPU在缓存中找不到要用数据,那么它就只能等待内存并且什么都不干。这样就会让效率变得极其的低。在以后的教程里我会更加深入地讲如何更高效地利用快速缓存(L1, L2, 和L3缓存)。
如果有什么建设性的批评的话请务必在下方留言。我在这里提前表示感谢!
脚注
function matmul2!(C::AbstractMatrix, A::AbstractMatrix, B::AbstractMatrix, fillzero=true)
fillzero && fill!(C, zero(eltype(C)))
m, p = size(A); n = size(B, 2)
@assert m == size(C, 1) && n == size(C, 2) && p == size(B, 1)
@inbounds for k in 1:p, i in 1:m, j in 1:n
C[i, j] += A[i, k]*B[k, j]
end
C
end