应该算是新人，对julia的理念非常感兴趣，不过运行官方在 juliabox 的 tutorial 中"julia is fast"一节的时候，发现官方例子：对 10^7 的随机数据进行求和的时候，都是是 numpy 获胜，想请教一下大家是怎么看待这个问题的呢？或者换句话说，在 python 蓬勃发展的今天，julia 对上 python 是否还有效率上的优势呢。
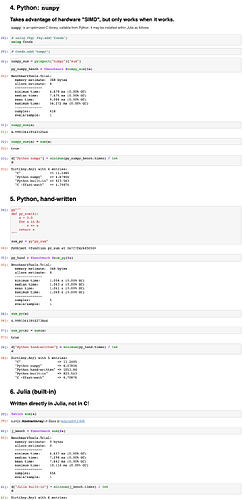
numpy的很多函数底层是C的，试想如果numpy没有这个函数，你会怎么办？
其实我觉得吧，只要不是大量的for循环，python也没什么问题。只要循环量一大python就蔫了。
再看julia，你自己可以用循环10^7求和，其速度已经和numpy很接近了。
这样就尽可能避免了“为了提高运算速度把某段代码用C实现”的问题。
其实cython就挺好，不过一调试就吐血。
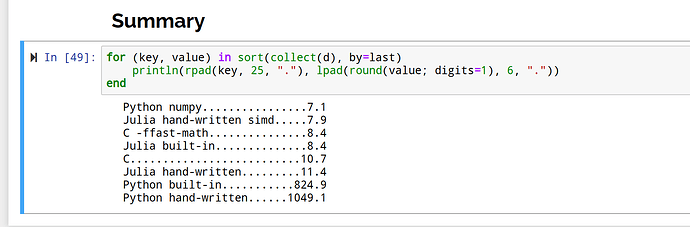
我看到的是 Julia 手写的简单 simd for-loop 能跟 numpy 这种成熟的库性能不相上下（前4个性能是同一水平，那 0.几 的性能差得放多大算力的机器上才有区别？）。
谢谢～我想明白啦
numpy和Julia的sum应该产生的机器码相差不大。这个教程想表达的是，在Julia里面你能写类似Python的语法，获得和numpy这样的C+Fortran的库相似的性能。
NumPy的max比Julia的maximum快不少。
julia> using PyCall
julia> @pyimport numpy as np
julia> using BenchmarkTools
julia> using Random; Random.seed!(1); a = rand(10^7); a[rand(1:10^7)] = NaN;
julia> @btime np.max($a)
5.631 ms (8 allocations: 368 bytes)
NaN
julia> @btime maximum($a)
7.159 ms (0 allocations: 0 bytes)
NaN
有些函数在NumPy确实快，这是不争的事实。坏处就是NumPy只是对Float64或者Float32快。而Julia可以用很多不同的数据类型。比如说Dual数字
julia> using ForwardDiff
julia> a = ForwardDiff.Dual.(rand(10^7÷2), rand(10^7÷2));
julia> @btime maximum($a)
17.865 ms (0 allocations: 0 bytes)
Dual{Nothing}(0.9999997371954783,0.07221970918741372)
你就直接得到maximum的微分了。你可能说maximum微分很简单，你可以自己算。但是如果你在一个很大的函数里用了maximum，我想你是不会想去写链式法则的。
如果有人说，Python也可以做自动微分。那么可以看看下面的例子。如果你是学物理或者工程的，测量的数据有误差，计算中也要去传播误差。那么可以这样
julia> using Measurements
julia> a = measurement.(rand(10^7÷2), rand(10^7÷2)); a[1:3]
3-element Array{Measurement{Float64},1}:
0.9741558410075197 ± 0.9935334559578708
0.5791363481531311 ± 0.19502598354585765
0.40606778803723254 ± 0.7092551723515295
julia> @btime maximum($a)
43.010 ms (0 allocations: 0 bytes)
0.999999852008173 ± 0.9144925086644928
那么更神奇的来了，你可以把不确定性和Dual数字结合，得到带有不确定性的微分。
julia> b = ForwardDiff.Dual.(a, a);
julia> @btime maximum($b)
1.307 s (64999987 allocations: 2.31 GiB)
Dual{Nothing}(0.999999852008173 ± 0.9144925086644928,0.999999852008173 ± 0.9144925086644928)
嘛。。。当然这个就很慢了2333。Julia的编译器还是有提升的空间的。