高斯求积简介

学科相关
1

高斯求积

高斯求积是常用的数值求积方法，这里主要介绍一下高斯-勒让得求积法则。我们都知道函数 f(x) 的积分可以用 n 个矩形的面积来逼近（如下图），一般会在函数 f(x) 上等间距采 n 个点的值 f(x_1), f(x_2), ... , f(x_n) ，然后分别乘以间隔（权重）得到面积，再累加求和得到积分。
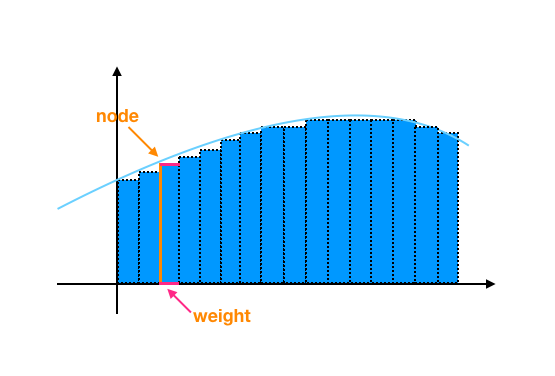
image

而数值求积的思路是找到一些点 x_i 以及合适的权重 w_i ，用 \sum w_if(x_i) 来逼近 f(x) 在 [-1,1] 的定积分。倘若我们随机选 4 个点 x_1, x_2, x_3, x_4 ，那么要使:point_down:对所有 f(x) 都成立：

\int_{-1}^{1} f(x)dx \approx w_1f(x_1) + w_2f(x_2) + w_3f(x_3) + w_4f(x_4)

现在，我们的目标是用 n 个点完美积分 n-1 阶多项式。可以分别令 f(x) 为张成多项式空间的一组基 (1, x, x^2, x^3) ：

2 = \int_{-1}^{1} 1dx \approx w_1 + w_2 + w_3 + w_4 \\ 0 = \int_{-1}^{1} xdx \approx w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 \\ \frac{2}{3} = \int_{-1}^{1} x^2dx \approx w_1x_1^2 + w_2x_2^2 + w_3x_3^2 + w_4x_4^2 \\ 0 = \int_{-1}^{1} x^3dx \approx w_1x_1^3 + w_2x_2^3 + w_3x_3^3 + w_4x_4^3 \\

这样就得到了一个线性方程组，4 个方程 4个权重 w_1, w_2, w_3, w_4 未知数，正好可以解出。如果我们选择 x_i 在 [-1,1] 上均匀分布，那么这就是牛顿-柯特斯积分。这里有一个 Julia 的例子：

julia> V(x) = [x[j]^(i-1) for i in eachindex(x), j in eachindex(x)]
V (generic function with 1 method)

julia> x = range(-1, stop=1, length=4)
-1.0:0.6666666666666666:1.0

julia> w = V(x)\[2, 0, 2/3, 0]
4-element Array{Float64,1}:
 0.24999999999999978
 0.7500000000000002
 0.7500000000000002
 0.24999999999999983

julia> f(x) = 1+15x+2x^2+12x^3
f (generic function with 1 method)

julia> w'f.(x)
3.333333333333334

F(x)|_{-1}^{1} = (x + \frac{15}{2} x^2 + \frac{2}{3} x^3 + 3x^4)|_{-1}^{1} = \frac{10}{3}

可以看到对于多项式，可以完美积分。下面是一个非多项式的例子，也可以得到不错的精度。

julia> w'cos.(x)  # cos(x) 在 [-1,1] 的积分是 2sin(1)
1.6875865724061767

julia> 2sin(1)
1.682941969615793

julia> w'sin.(x)  # sin(x) 在 [-1,1] 的积分是 0
2.7755575615628914e-17

高斯-勒让得求积

上面选取的点，权重以及基 (1, x, x^2, x^3) 都比较随意，合理的选择就可以做到用更少的点来获得更精确的估计。首先 (1, x, x^2, x^3) 不是正交基（我们现在定义多项式内积的定义是: \langle p, q \rangle = \int_{-1}^{1} p(x) q(x) dx ），我们可以对其作格拉姆-施密特正交化（Gram-Schmidt）正交化得到另一组基 (L_1, L_2, ..., L_n) 。

任何一个 2n-1 阶的多项式都可以被分解成 p_{2n-1}(x) = q_{n-1}(x)L_n(x) + r_{n-1}(x) ，其中下标表示多项式的阶数。由于 L_n(x) 是由一组正交基 (L_1, L_2, ..., L_n) 的线性组合， q_{n-1}(x) 又可以表示为 (L_1, L_2, ..., L_{n-1}) 的线性组合，因此 L_n(x) 与 q_{n-1}(x) 正交，那么我们有积分

\int_{-1}^{1} p_{2n-1}(x) dx = \int_{-1}^{1} q_{n-1}(x)L_n(x)dx + \int_{-1}^{1}r_{n-1}(x) dx \\ = 0 + \int_{-1}^{1} r_{n-1}(x) dx.

在这个基下， p_{2n-1} 和 r_{n-1}(x) 的积分相等，我们只需要对 n-1 阶多项式积分就能得到 2n-1 阶多项式的积分。

现在我们已经选好了基，下一步是选点，按照高斯求积的思路，选取的这些点最终要使 \sum w_if(x_i) 完美计算 p_{2n-1}(x) 的积分，所以 p_{2n-1}(x) 和 r_{n-1}(x) 多项式应该在这些点上相等。

如果我们取 L_n(x) 的根，这个时候我们有 q_{n-1}(x_i)L_n(x_i) = 0 ，和 p_{2n-1}(x_i)=r_{n-1}(x_i) ，其中 x_i 就是积分要取值的点。 那么就应该将点选为满足 L_n(x_i)=0 条件的。

下面是用Golub-Welsch算法计算高斯-勒让得的点和权重。

julia> using LinearAlgebra

julia> function gauss_quad(n)
           β = @. .5/sqrt(1-(2*(1:n-1))^(-2.))
           T = SymTridiagonal(zeros(n), β)
           D, V = eigen(T)
           i = sortperm(D); x = D[i]
           w = 2*view(V, 1, i).^2
           x, w
       end
gauss_quad (generic function with 1 method)

julia> x, w = gauss_quad(4)
([-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855])

julia> w'cos.(x)
1.6829416886959736

julia> 2sin(1)
1.682941969615793

我们可以看到虽然仅仅用了四个点，但是计算得十分准确。

数值实验

using Plots; gr()
using SpecialFunctions
using LinearAlgebra
function newton_cotes(m)
    V(x) = [x[j]^(i-1) for i in eachindex(x), j in eachindex(x)] # transposed Vandermonde matrix
    rhs(m) = [((-1)^n + 1)/(n+1) for n in 0:m-1]
    x = range(-1, stop=1, length=m)
    w = V(x)\rhs(m)
    return x, w
end
function gauss_quad(n)
    β = @. .5/sqrt(1-(2*(1:n-1))^(-2.))
    T = SymTridiagonal(zeros(n), β)
    D, V = eigen(T)
    i = sortperm(D); x = D[i]
    w = 2*view(V, 1, i).^2
    return x, w
end
f(x) = ℯ^(-x^2)
sol = √pi*erf(1) # integral of f from -1 to 1
ns = 2:50
newton_errs = map(ns) do n
    x, w = newton_cotes(n)
    return err = abs(sol - w'f.(x))
end
gauss_errs = map(ns) do n
    x, w = gauss_quad(n)
    return err = abs(sol - w'f.(x)) + eps() # machine epsilon to aviod exact 0
end
plot(ns, newton_errs, lab="Newton-Cotes")
plot!(ns, gauss_errs, lab="Gauss-Legendre", dpi=300)
yaxis!("Error", :log10)
xaxis!("Number of nodes")
savefig("$(homedir())/quad_plt.png")

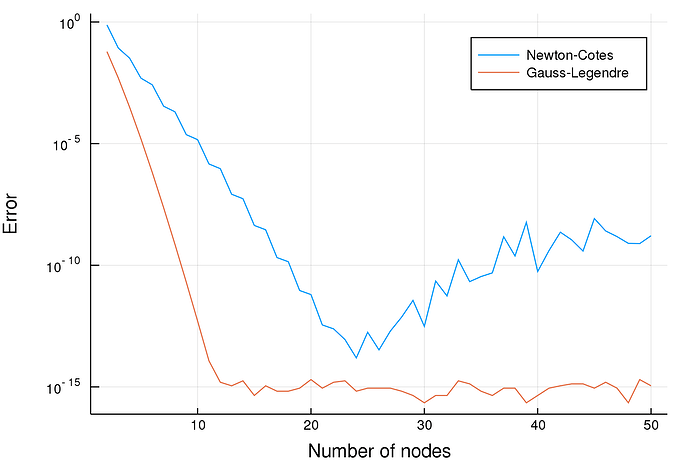
值得注意的是牛顿-柯特斯（Newton-Cotes）收敛的速度不但比高斯-勒让得（Gauss-Legendre）收敛的速度慢，而且因为龙格现象（Runge’s phenomenon）导致牛顿-柯特斯在浮点运算下不会收敛。

quad_plt
quad_plt1800×1200 99.8 KB

延伸

注意高斯求积要求积分区间为 [-1,1] ，实际应用需要用变区间法则将积分区间转换到这个范围。

\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{2}}\sum _{i=1}^{n}w_{i}f\left({\frac {b-a}{2}}x_{i}+{\frac {a+b}{2}}\right).

感谢

本文大部分由 @Gnimuc 整理和撰写， @scheme 修改。

8 个赞
3

有没有人对上面写的Golub-Welsch算法或者计算Newton-Cotes的方法有疑问？

4

首先膜拜大神下，算法确实精准且快速，但是，完全看不懂的说，如果有时间，还请大神点化，谢谢，尤其是这个权重的得出，和积分范围的改变如何操作，谢谢，并再次膜拜大神！！！

5

变化积分范围直接用这个公式就可以了。比如说从0积分到10

julia> using LinearAlgebra

julia> function gauss_quad(n)
           β = @. .5/sqrt(1-(2*(1:n-1))^(-2.))
           T = SymTridiagonal(zeros(n), β)
           D, V = eigen(T)
           i = sortperm(D); x = D[i]
           w = 2*view(V, 1, i).^2
           return x, w
       end
gauss_quad (generic function with 1 method)

julia> f(x) = ℯ^(-x^2)
f (generic function with 1 method)

julia> x, w = gauss_quad(30);

julia> b = 10.; a = 0.;

julia> (b-a)/2 * w' * @. f((b-a)/2*x + (a+b)/2)
0.8862269254527585

你知道了高斯求积点的位置就是正交多项式的根，所以可以求出积分要取值的点。而且你还知道当被积分函数是小于 n 阶多项式的时候，我们要有精准的积分。你可以列出如下等式

\displaystyle \int _{-1}^{1}\tau^m\,d\tau = \sum_{i=1}^{n}w_{i} x_{i}^m, \quad m = 0, 1, ..., n-1

这个时候，令

\displaystyle \ell_i(t) = \prod^{n}_{k=1,k\ne i} \frac{t-x_k}{x_i - x_k}, \quad i=1,2,...,n,

也就是拉格朗日多项式。我们有

\displaystyle \sum^n_{i=1} \ell_i(t)p(x_i) = p(t)

对于任何小于 n 阶的多项式 p （这就是拉格朗日插值法）。我们现在令 w_i = \int_{-1}^{1} \ell(\tau)\, d\tau

\displaystyle \sum_{i=1}^n w_i x_i^m = \sum_{i=1}^n \int_{-1}^{1} \ell_i(\tau)\, d\tau \cdot x_i^m = \int_{-1}^1 \left(\sum^n_{i=1} \ell_i(\tau) x_i^m \right)\, d\tau = \int_{-1}^{1} \tau^m \, d\tau, \quad m=0,1,...,n-1.

所以，权重就是

\displaystyle w_i = \int_{-1}^{1} \prod^{m}_{k=1,k\ne i} \frac{t-x_k}{x_i - x_k} \, dt, \quad i=1,2,...,n.

上面的Golub-Welsch算法里得到点和权重的方法就是利用Jacobi矩阵的特征多项式的三项递归特性。

2 个赞
7

多谢指点，开始了然，多谢

8

您好，想问一下您关于复合高斯求积中的“延伸”中积分区间是转换到哪一个范围？