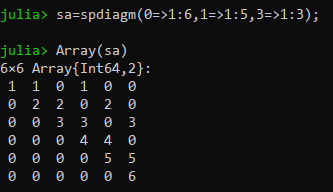
采用松弛迭代法求线性方程组(迭代法):
Ax=b
其中A为(nxn,nxn)的系数矩阵,x为(nxn,1)的未知向量,b为(nxn,1)的常量
#-----------------------------第一个需要优化的部分
首先新建一个用超松弛迭代法求解线性方程组的函数
X为迭代初始值
function sor(A,b,X,mn,w,ww)
# sor - Description
#
# Syntax: output = myFun(input)
#
# mn = 最大迭代次数
# w = 误差精度
# ww = 松弛因子
it = 1 # 迭代次数初值
D = Diagonal(Diagonal(A))
L = LowerTriangular(-A)+D
U = UpperTriangular(-A)+D
M = inv(D-ww*L)*((1-ww)*D+ww*U) # 迭代矩阵
g = ww*inv(D-ww*L)*b # 迭代格式中的常数项
while it <= mn
x = M*X+g
if norm(x-X,Inf) < w
# disp('迭代次数为')
# in
return it,x
end
X = x
it += 1
end
println("最大迭代次数内不收敛!")
end
#------------------第二部分需要优化的
然后,组建系数矩阵A和常量向量b
其中,A的形式为:
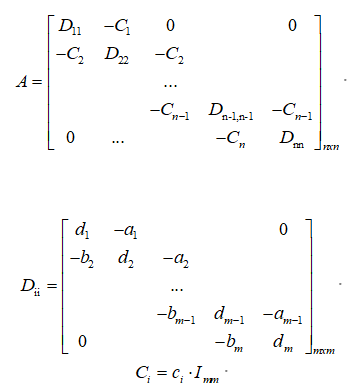
我自己的代码性能很差,见下:
for s = 0:(n-1)
for t = 1:div(m,n_b)-1
A[t+(div(m,n_b)-1)*s, t+(div(m,n_b)-1)*s] = Coe_D[(k-1)*div(m,n_b)+t+1]
if t == 1
A[t+(div(m,n_b)-1)*s, t+1+(div(m,n_b)-1)*s] = -Coe_A[(k-1)*div(m,n_b)+t+1]
elseif t == div(m,n_b)-1
A[t+(div(m,n_b)-1)*s, t-1+(div(m,n_b)-1)*s] = -Coe_B[(k-1)*div(m,n_b)+t+1]
else
A[t+(div(m,n_b)-1)*s, t+1+(div(m,n_b)-1)*s] = -Coe_A[(k-1)*div(m,n_b)+t+1]
A[t+(div(m,n_b)-1)*s, t-1+(div(m,n_b)-1)*s] = -Coe_B[(k-1)*div(m,n_b)+t+1]
end
if s == 0
A[t+(div(m,n_b)-1)*s, t+(div(m,n_b)-1)*(s+1)] = -2*Coe_C[(k-1)*div(m,n_b)+t+1]
elseif s == n-1
A[t+(div(m,n_b)-1)*s, t+(div(m,n_b)-1)*(s-1)] = -Coe_C[(k-1)*div(m,n_b)+t+1]
else
A[t+(div(m,n_b)-1)*s, t+(div(m,n_b)-1)*(s+1)] = -Coe_C[(k-1)*div(m,n_b)+t+1]
A[t+(div(m,n_b)-1)*s, t+(div(m,n_b)-1)*(s-1)] = -Coe_C[(k-1)*div(m,n_b)+t+1]
end
B[t+(div(m,n_b)-1)*s, 1] = Coe_F[(k-1)*div(m,n_b)+t+1]
end
end
其实这个感觉应该用分块矩阵,然后用三对角矩阵
(Tridiagonal(dl::V, d::V, du::V) where V)组建系数矩阵A比较好
但不知道分块矩阵怎么实现
最后求解,
function pressure(k::Int64)
for s = 0:19
for t = 1:19
A[t+19*s, t+19*s] = Coe_D[(k-1)*20+t+1]
if t == 1
A[t+19*s, t+1+19*s] = -Coe_A[(k-1)*20+t+1]
elseif t == 19
A[t+19*s, t-1+19*s] = -Coe_B[(k-1)*20+t+1]
else
A[t+19*s, t+1+19*s] = -Coe_A[(k-1)*20+t+1]
A[t+19*s, t-1+19*s] = -Coe_B[(k-1)*20+t+1]
end
if s == 0
A[t+19*s, t+19*(s+1)] = -2*Coe_C[(k-1)*20+t+1]
elseif s == n-1
A[t+19*s, t+19*(s-1)] = -Coe_C[(k-1)*20+t+1]
else
A[t+19*s, t+19*(s+1)] = -Coe_C[(k-1)*20+t+1]
A[t+19*s, t+19*(s-1)] = -Coe_C[(k-1)*20+t+1]
end
B[t+19*s, 1] = Coe_F[(k-1)*20+t+1]
end
end
(it, p_p) = sor(A, B, XX, mn, w, ww)
end
求出it迭代次数和p_p(未知向量x)
如果没有 (it, p_p) = sor(A, B, XX, mn, w, ww)这行
代码运行时间:
160.853 μs (3644 allocations: 56.94 KiB)
如果加上 (it, p_p) = sor(A, B, XX, mn, w, ww)
代码运行时间:
迭代次数2597,436.086 ms (11505 allocations: 44.78 MiB)