求教一个问题：juno中的@profiler 用法及代码优化

综合讨论区 性能优化
1

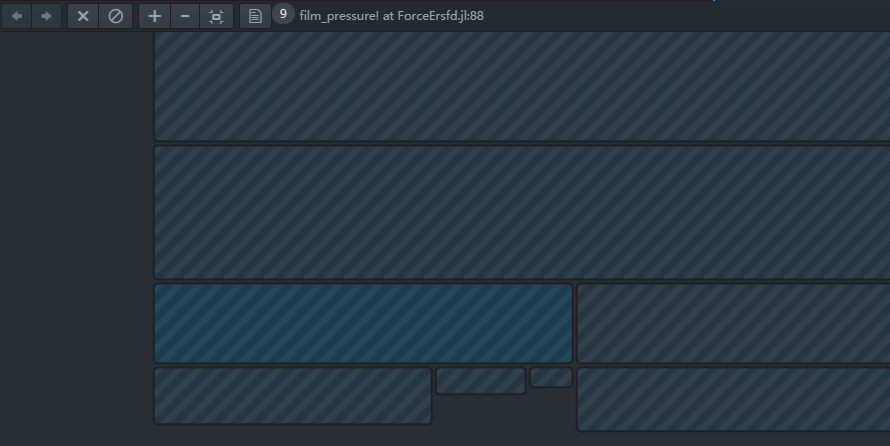
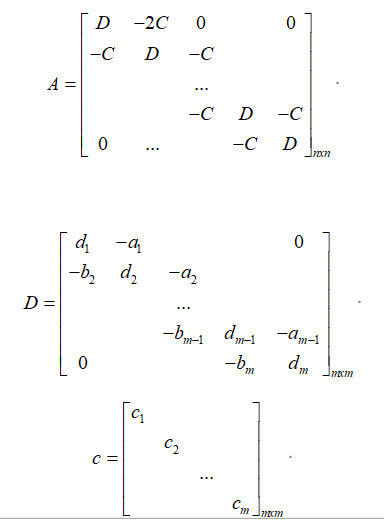各位好，请教一个问题，希望各位高手赐教，拜托拜托！
实质问题是求解线性方程组Ax=b，即x=A\b，矩阵A为：

image
image384×523 4.08 KB

'''julia
function film_pressure!(pless, Coe, k, n)
    Coe_A,Coe_B,Coe_C,Coe_D,Coe_E,Coe_F,Coe_G = Coe
    lv = repeat([Coe_B[3+20*(k-1):20*k]; 0], n)
    lv = lv[1:end-1]
    dv = repeat(Coe_D[2+20*(k-1):20*k], n)
    uv = repeat([Coe_A[2+20*(k-1):20*k-1]; 0], n)
    uv = uv[1:end-1]
    rv = repeat(Coe_C[2+20*(k-1):20*k], n)
    rv = rv[1:end-19]
    sv = [2*rv[1:19]; rv[20:end]]
    AA = Array(spdiagm(-19=>-rv, -1=>-lv, 0=>dv, 1=>-uv, 19=>-sv))
    BB = repeat(Coe_F[20*(k-1)+2:20*k], n)
    TT = AA\BB
    @.TT[TT<0] = 0
    sp = (reshape(TT,19,20))'
    pless[1:20,20(k-1)+2:20k] = sp
    return nothing
end
'''

代码中AA是矩阵A，BB是b，TT为x
运行时间慢，并且有不少gc
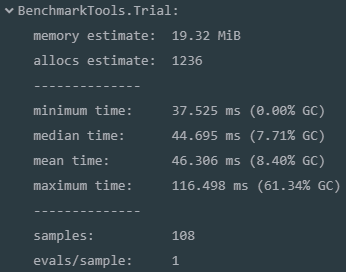
image
运行@profiler

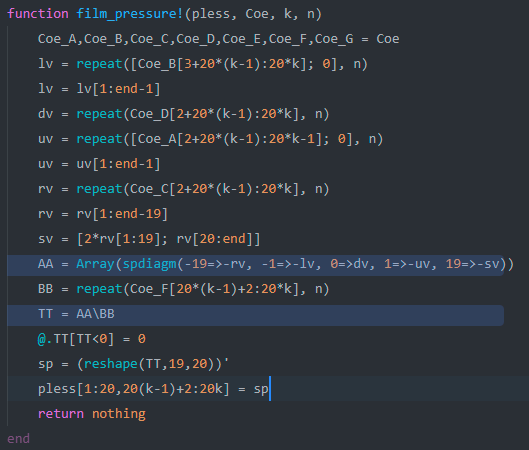
image
image890×446 16.8 KB

image
高亮的两行代码backtraces(samples)数分别为9
是不是表明主要的性能问题在这2行中
如果是的话，能不能给点优化建议，这已经是我所知道的最快方法了，希望各位指点下，拜托拜托，谢谢！

2

为什么 Array(spdiagm(-19=>-rv, -1=>-lv, 0=>dv, 1=>-uv, 19=>-sv))不直接AA=spdiagm(-19=>-rv, -1=>-lv, 0=>dv, 1=>-uv, 19=>-sv)？

3

为什么要用字典呢 -19=>-rv

4

因为一开始我运行了一个小的矩阵求解，发现用稀疏矩阵求解还慢一点，就把稀疏矩阵转为array了，让我十分不解
后来发现矩阵大的时候还是稀疏矩阵快
‘’’ julia
using BenchmarkTools, LinearAlgebra, SparseArrays
a = [1;1;1;1]
b= [1;1;1]
c = diagm(0=>a, 1=>b)
d = [2;2;2;1]
@benchmark sol = c\d
‘’’
运行时间380ns
‘’’
e = spdiagm(0=>a, 1=>b)
@benchmark sol2 = e\d
‘’’
运行时间640ns

5

diagm的用法就是字典啊

6

emmm，当然了。稀疏矩阵当然是在大的是时候才快。

7

好的，谢谢指点！

8

这个不是字典，这个是Pair，只是字典也使用Pair初始化而已