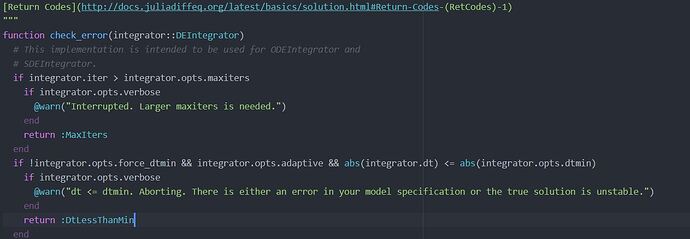
计算出错:
┌ Warning: dt <= dtmin. Aborting. There is either an error in your model specification or the true solution is unstable.
└ @ DiffEqBase C:\Users\好兔子.julia\packages\DiffEqBase\cPqrj\src\integrator_interface.jl:156
DiffEqBase C:\Users\好兔子.julia\packages\DiffEqBase\cPqrj\src\integrator_interface.jl:156:
如果不加这段,就不会报错。
#
using PyPlot
using DifferentialEquations
using LinearAlgebra
using CSV,DataFrames
###########################################################################################
INPUT
###########################################################################################
module msh
using PyPlot
export plotMesh
struct Mesh
coords
function Mesh(n1,n2)
@assert (n1 > 0 && n2 > 0) "Mesh arguments must be positive"
coords = createCoords(n1,n2)
new(coords)
end
end
function createCoords(n1,n2)
#Fill coords array
coords = zeros(2,n1*n2);
cnt = 1
for i = 1:n2
for j = 1:n1
coords[1:2,cnt] = [j-1,i-1]
cnt = cnt+1
end
end
return coords
end
function plotMesh(m::Mesh,c::String)
#Plot coordinates
for i = 1:size(m.coords)[2]
plot(m.coords[1,i],m.coords[2,i],marker="o",color =c, markersize = 10)
end
end
end
#number of particles will be n*n
N = 10*18
#set up mesh
m = msh.Mesh(10,18)
npull = 40 #number of elements being pulled at a constant speed
nhold = 40 #number of elements being held at their initial position
#m.coords[2,1:nhold]=m.coords[2,1:nhold]+0.99*ones(size(m.coords[2,1:nhold]))
#m.coords[2,131:N]=m.coords[2,131:N]-0.99*ones(size(m.coords[2,131:N]))
#Set time interval [0,maxT]
maxT = 3e-6
E=25000000000
v=0.26
k=E/(3*(1-2v))
r=4
h=1
c=210*E/(5*pi*r^3)
u=E/(2+2v)
#Set up matrix of spring constants
global K
K = zeros(N,N)
for i = 1:N
for j = i+1:N
K[i,j] = c*(1-(norm(m.coords[:,i] - m.coords[:,j],2)/r)^2)^2
if norm(m.coords[:,i] - m.coords[:,j],2)>4
K[i,j]=0
end #compute 2-norm because why not
K[j,i] = K[i,j]
end
end
#strengthen bond to the boundary nodes
##################################################################################################
#count the number of bonds each element has
global nbonds = Dict{Float64, Array{Float64,2}}()
nbonds[0.] = N*ones(N,1)
c1 = [0 -100000]
s0=125/(6*u/pi+16/(9*pi^2)*(k-2u)*r)
function f(x,p,t)
global K
H = ones(size(K))
s=ones(size(K))
xh = [m.coords[1,1:nhold] m.coords[2,1:nhold];
hcat(x[1:N-npull-nhold], x[N-npull-nhold+1:2*(N-npull-nhold)]);
(c1[1]*t*ones(size(m.coords[1,N-npull+1:N]))+m.coords[1,N-npull+1:N]) (c1[2]*t*ones(size(m.coords[2,N-npull+1:N]))+m.coords[2,N-npull+1:N])]'
for i = 1:N
for j = i+1:N
s[i,j]=(norm(xh[:,i]-xh[:,j])-norm(m.coords[:,i] - m.coords[:,j],2))/norm(m.coords[:,i] - m.coords[:,j],2)
if s[i,j] > sqrt(s0)
H[i,j] = H[j,i] = 0
end
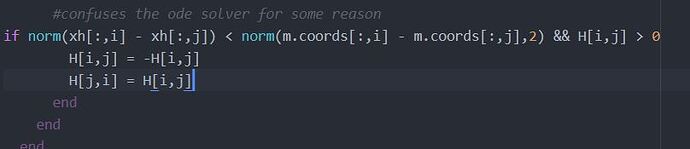
#make particles repulse each other/try to enforce order
#confuses the ode solver for some reason
if norm(xh[:,i] - xh[:,j]) < norm(m.coords[:,i] - m.coords[:,j],2) && H[i,j] > 0
H[i,j] = -H[i,j]
H[j,i] = H[i,j]
end
end
end
K=K.*H
#recalculate the number of bonds
global nbonds
nbonds[t] = sum(K.!=0, dims=2)
#Create stiffness matrix
A = zeros(N-npull-nhold,N-npull-nhold)
for i = 1:N-npull-nhold
A[i,i] = sum(K[i+nhold,1:N]) #diagonal is special :)
for j = 1:N-npull-nhold
if(i!=j) A[i,j] = -K[i+nhold,j+nhold] end
end
end
cf=DataFrame(A)
CSV.write("a.csv",cf)
#Create "forcing" term
B = zeros(2*(N-npull-nhold),1)
for i = 1:N-npull-nhold
B[i] = sum((c1[1]*t*ones(size(m.coords[1,N-npull+1:N])) + m.coords[1,N-npull+1:N]).*K[i+nhold,N-npull+1:N]) + sum(K[i+nhold, 1:nhold].*m.coords[1,1:nhold])
B[i+N-npull-nhold] = sum((c1[2]*t*ones(size(m.coords[2,N-npull+1:N])) + m.coords[2,N-npull+1:N]).*K[i+nhold,N-npull+1:N]) + sum(K[i+nhold, 1:nhold].*m.coords[2,1:nhold])
end
y = [A*x[1:N-npull-nhold]+B[1:N-npull-nhold];
A*x[N-npull-nhold+1:2*(N-npull-nhold)]+B[N-npull-nhold+1:2*(N-npull-nhold)]]''
return [x[2*(N-npull-nhold)+1:end]; y]
end
#Solve system of second order ODE using ode45
y0 = [m.coords[1,nhold+1:N-npull];
m.coords[2,nhold+1:N-npull];
zeros(2*(N-npull-nhold))] #initial conditions
#initial positions given by mesh, initial speed set to zero
#tout,yout = ode45(f, y0,[0:0.1:maxT;])
prob = ODEProblem(f, y0,(0.0,maxT))
#alg = Tsit5()
sol = solve(prob)
tout = sol.t
yout = sol.u
ys = hcat(yout...)'
print("Number of timesteps: ", size(tout)[1], "\n")