如题，在数学建模（比如数模比赛），或者在项目中需要做符号公式推导，而又希望能把公式等化成Julia表达式代入下一步数值运算的CAS扩展包有哪些？
大致要求如下：
1.功能上的：
代数化简，三角函数化简，
解线性方程组
解符号矩阵，解矩阵特征值
符号求微积分，求解微分方程（组）
向量场图/相图（也许可以用非CAS包）
2.兼容性上
可以从Julia本身的一些数据结构，如Expr作为表达式输入，本身的Expr做输出，这样可以在符号推导后算一下数值。
3.可靠性
有人维护的，尽量是使用Julia写的（不考虑一直调用SimPy）
我找到的一些有
nemoCAS:
http://www.nemocas.org/
abstractAlgrbra:
https://github.com/Nemocas/AbstractAlgebra.jl
symata:
linearexpressions:
各位有用过这些的请给点建议。
刚刚读了一些docu，感觉刚才说的‘以Julia编写的’有点苛刻。
AbstractAlgebra和Nemo似乎更关心分析一些。然后那个linearexpression似乎还不是很完善。
现在可以供调用的有Maxima，Sympy和SageMath，这三个在开源CAS里算不错的了。
然而我不想用Maxima调用，原因很多。。。主要是Maxima近年生态不是很好
Sympy似乎好一些，而且有人用更Julian的方法写了函数
https://github.com/JuliaPy/SymPy.jl/blob/master/examples/tutorial.md
对于更强大的SageMath，似乎要麻烦一些
当然你也可以自己写（重新发明轮子）
这个CAS的话题我记得好像油管上有视频讲过，也许在AA完善之前大家都在用Sympy.
向量场图可以用 PyPlot.jl 包的 streamplot 函数绘制，在其他的绘图包我也没有找到以实现相同功能的函数。
Nemo 还有与之相关的 Hecke 在我看来不算是 CAS，感觉只是实现了一些数学上的诸如群、环、域之类的代数结构。感觉大多数都是调用其他语言的包。
最近有一个Grassmann代数的包，可以补充一些feature。不过总的来说Julia需要大家造（纯Julia的）轮子来发挥语言本身的优势，目前很多方向还没有到什么都有的阶段。
看到 slack 上有人讨论这个 Slack
The OSCAR project develops a comprehensive open source computer algebra system for computations in algebra, geometry, and number theory.
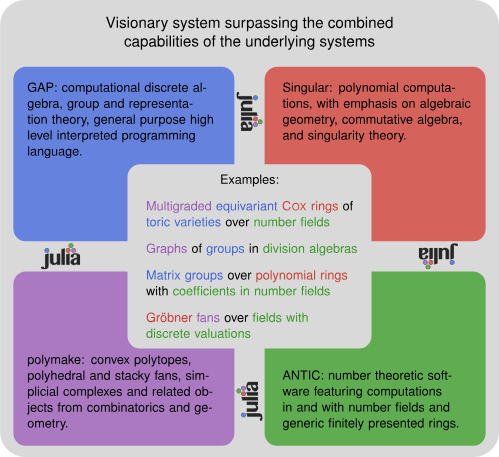
The project builds on and extends the four cornerstone systems
感谢。
是的，Julia的数据结构其实对Symbolic Math 是足够强大的，只是原先的主要工作不是在上面完成的。
绘图的算法其实还比较好写，（vector field 和implicit plot，cob web 等等功能其实可以自己在现有的plot上面改造）。主要是计算机代数。
纯数学的很多东西我不懂。
最近找到了 Certik写的symengine.jl, 是symengine 计划的一部分（当然也是调用c，而不是纯Julia）。
怎么说呢，感觉这是一个加速般的sympy。在试试看好不好用（最近正在艰难的从SageMath往Sympy切换）