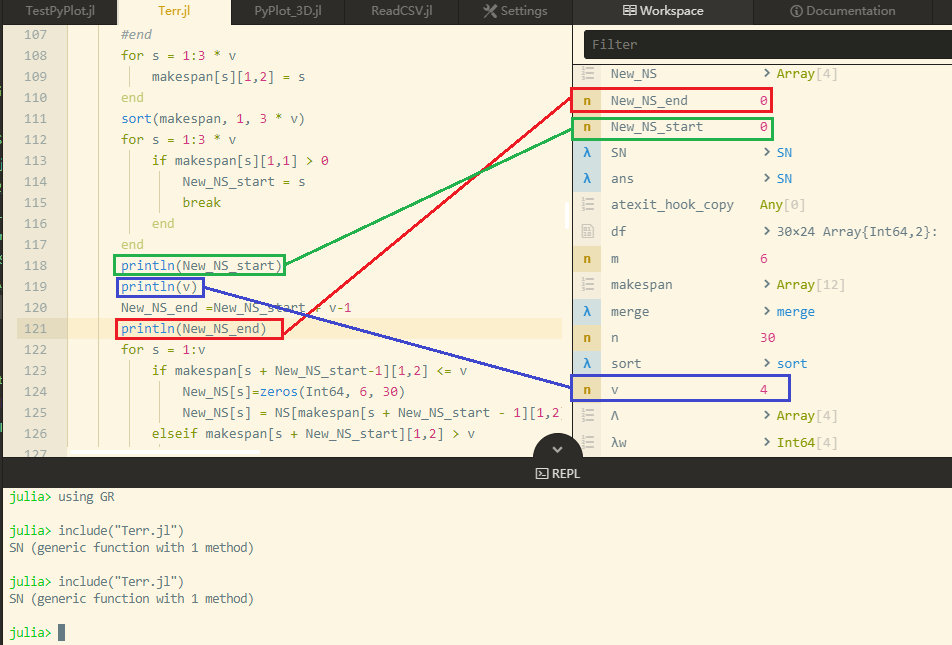
第118行加号运算为什么不成立?我用Debugger.Jl调试发现
1|debug> w add (New_NS_start,New_NS_end,New_NS_start + v-1)
1] (New_NS_start, New_NS_end, (New_NS_start + v) - 1): (1, 3, 4)
也就是说v=4,New_NS_start=1,New_NS_end=3,但是New_NS_end =New_NS_start + v-1啊
代码如下:
# This Fruit Fly Optimization Algorithm
v = 4#The numble of all scanrios
Λ = Vector{Array}(undef, v)#Λ is the set of scanrios
NS = Vector{Array}(undef, v)#Each NS is a individual of a population, that is a schedule solution
New_NS = Vector{Array}(undef, v)
Mc = 1#The crite machine
Mm = 1
Mc_completion_time = 0
Mm_completion_time = 0
NS_neighborhood = Vector{Array}(undef, 2 * v)
λw = Vector{Int64}(undef, v) #The worst-case scanrio
makespan = Vector{Array}(undef, 3 * v)
New_NS_start = 0
New_NS_end=0
Maxgen = 200
using DelimitedFiles
df = readdlm("D:/home/src/papercode/testdf.txt", ',', Int64;header = false)
for λ = 1:4 #The λ th scanrio
Λ[λ] = zeros(Int64, 6, 30)
for i = 1:6#The ith machine
for j = 1:30#The jth job
Λ[λ][i,j] = df[j,i + 6 * (λ - 1)]
end
end
end
(m, n) = size(Λ[1])
function FOA(Λ::Vector{Array}, Maxgen::Int64)
#----------------------------------------------------------------------------------------------
for iter = 1:Maxgen
#Initialization
for λ = 1:v
NS[λ] = zeros(Int64, 6, 30)
for j = 1:n
NS[λ][1,j] = 1
machine_min = 1
for i = 1:m
if Λ[λ][i,j] < Λ[λ][machine_min,j]
NS[λ][machine_min,j] = 0
machine_min = i
NS[λ][machine_min,j] = 1
end
end
end
end
#--------------------------------------------------------------------------------------------
#SS_WN(λ) under the worst-case neighborhood
for s = 1:v#For each schedule solution s
λw[s] = 1 #The worst-case
makespan[s] = zeros(Int64, 1, 2)
for i = 1:m,j = 1:n
makespan[s][1,1] = makespan[s][1,1] + Λ[λw[s]][i,j] * NS[s][i,j]
end
for λw_of_s = 1:v#Find the worst-case scanrio of the schedule solution s
makespan_of_s_temp = 0
for i = 1:m,j = 1:n
makespan_of_s_temp = makespan_of_s_temp + Λ[λw_of_s][i,j] * NS[s][i,j]#Cumpute the makespan of the schedule solution under the scanrio λw_of_s
end
if makespan_of_s_temp > makespan[s][1,1]
λw[s] = λw_of_s
makespan[s][1,1] = makespan_of_s_temp
end
end
SN(λw[s], s)
end
#------------------------------------------------------------------------------------------
#Collaborative Vision-Based Search
for s = 1:v
makespan[v + s] = zeros(Int64, 1, 2)
makespan[2 * v + s] = zeros(Int64, 1, 2)
end
for s_temp = 1:2 * v#Delete the repeated individual
same = 0#Same=1 says that the s_tempth neighborhood is repeated Same=1,说明NS_neighborhood(s_temp)是多余的
for s = 1:v
if NS[s] == NS_neighborhood[s_temp]
same = 1
break
end
end
if same == 0
if (s_temp >= 1) && (s_temp <= v)
for i = 1:m,j = 1:n
makespan[v+s_temp][1,1] = makespan[v+s_temp][1,1] + Λ[λw[s_temp]][i,j] * NS_neighborhood[s_temp][i,j]
end
elseif (s_temp >= v + 1) && (s_temp <= 2 * v)
for i = 1:m,j = 1:n
makespan[v + s_temp][1,1] = makespan[v + s_temp][1,1] + Λ[λw[s_temp - v]][i,j] * NS_neighborhood[s_temp][i,j]
end
end
else
makespan[v + s_temp][1,1] = -1
end
end
# for s = 1:v
# if NS[s] == NS_neighborhood[s + v]
# makespan[v + s][1,1] = -1
# elseif NS[s] == NS_neighborhood[s + 2 * v]
# makespan[2 * v + s][1,1] = -1
#else
# makespan[v + s][1,1] = 0
# makespan[2 * v + s][1,1] = 0
# for i = 1:m,j = 1:n
# makespan[v + s][1,1] = makespan[v + s][1,1] + Λ[λw[s]][i,j] * NS_neighborhood[s][i,j]
# makespan[2 * v + s][1,1] = makespan[2 * v + s][1,1] + Λ[λw[s]][i,j] * NS_neighborhood[v + s][i,j]
#end
# end
#end
for s = 1:3 * v
makespan[s][1,2] = s
end
sort(makespan, 1, 3 * v)
for s = 1:3 * v
if makespan[s][1,1] > 0
New_NS_start = s
break
end
end
New_NS_end =New_NS_start + v-1
for s = 1:v
if makespan[s + New_NS_start-1][1,2] <= v
New_NS[s]=zeros(Int64, 6, 30)
New_NS[s] = NS[makespan[s + New_NS_start - 1][1,2]]
elseif makespan[s + New_NS_start][1,2] > v
New_NS[s]=zeros(Int64, 6, 30)
New_NS[s] = NS_neighborhood[makespan[s + New_NS_start-1][1,2]-v]
end
end
for s = 1:v
NS[s] = New_NS[s]
end
#-------------------------------------------------------------------------------------------------------
end
return makespan[New_NS_start][1], NS[1,1]
end
#--------------------------------------------------------------------------------------------------------
#采用分治算法进行排序
function sort(makespan::Vector{Array}, low::Int64, top::Int64)
if top - low > 1
mid = (low + top) ÷ 2
sort(makespan, low, mid)
sort(makespan, mid + 1, top)
merge(makespan, low, mid, top)
end
end
function merge(makespan::Vector{Array}, low::Int64, mid::Int64, top::Int64)
n1 = mid - low + 1
n2 = top - mid
L = Vector{Array}(undef, n1)
R = Vector{Array}(undef, n2)
for i = 1:n1
L[i]=zeros(Int64, 1, 2)
L[i][1,1] = makespan[low + i - 1][1,1]
L[i][1,2] = makespan[low + i - 1][1,2]
end
for j = 1:n2
R[j]=zeros(Int64, 1, 2)
R[j][1,1] = makespan[mid + j][1,1]
R[j][1,2] = makespan[mid + j][1,2]
end
i = 1
j = 1
for k = low:top
if (i<=n1&&j<=n2)&&(L[i][1,1] <= R[j][1,1])
makespan[k][1,1] = L[i][1,1]
makespan[k][1,2] = L[i][1,2]
i = i + 1
elseif (i<=n1&&j<=n2)&&(L[i][1,1] > R[j][1,1])
makespan[k][1,1] = R[j][1,1]
makespan[k][1,2] = R[j][1,2]
j = j + 1
elseif i>n1&&j<=n2
makespan[k][1,1] = R[j][1,1]
makespan[k][1,2] = R[j][1,2]
j = j + 1
elseif j>n2&&i<=n1
makespan[k][1,1] = L[i][1,1]
makespan[k][1,2] = L[i][1,2]
i = i + 1
end
end
end
#---------------------------------------------------------------------------------------------
#Construct single neighborhood
function SN(λw_SN::Int64, s_SN::Int64)
Mc_completion_time = 0
Mm_completion_time = 0
Mc = 1
Mm = 1
for j = 1:n
Mc_completion_time = NS[s_SN][Mc,j] * Λ[λw_SN][Mc,j] + Mc_completion_time
end
Mm_completion_time = Mc_completion_time
for i = 1:m
M_temp::Int64 = 0
for j = 1:n
M_temp = NS[s_SN][i,j] * Λ[λw_SN][i,j] + M_temp
end
if M_temp > Mc_completion_time
Mc = i
Mc_completion_time = M_temp
elseif M_temp < Mm_completion_time
Mm = i
Mm_completion_time = M_temp
end
end
#IO
NS_neighborhood[s_SN] = zeros(Int64, 6, 30)
NS_neighborhood[s_SN + v] = zeros(Int64, 6, 30)
for i = 1:m,j = 1:n
NS_neighborhood[s_SN][i,j] = NS[s_SN][i,j]
NS_neighborhood[v + s_SN][i,j] = NS[s_SN][i,j]
end
for j = 1:n
if NS_neighborhood[s_SN][Mc,j] > 0
NS_neighborhood[s_SN][Mc,j] = 0
NS_neighborhood[s_SN][Mm,j] = 1
break
end
end
#SO
for i = 1:m
if (i != Mm) && (i != Mc)
for j = 1:n
if NS_neighborhood[s_SN + v][Mc,j] > 0
NS_neighborhood[s_SN + v][Mc,j] = 0
NS_neighborhood[s_SN + v][i,j] = 1
break
end
end
break
end
end
end
#-------------------------------------------------------------------------------------------
其中D:/home/src/papercode/testdf.txt的内容如下:
2,4,3,7,8,2,7,8,5,1,5,5,2,4,3,7,8,2,7,8,5,1,5,5
1,6,4,6,3,1,1,7,4,1,9,6,1,6,4,6,3,1,1,7,4,1,9,6
2,4,9,8,9,2,1,1,8,1,6,6,2,4,9,8,9,2,1,1,8,1,6,6
4,9,1,1,4,3,2,8,3,5,9,1,4,9,1,1,4,3,2,8,3,5,9,1
5,3,3,8,1,4,4,7,1,8,1,9,5,3,3,8,1,4,4,7,1,8,1,9
5,5,2,4,4,9,6,9,5,9,2,6,5,5,2,4,4,9,6,9,5,9,2,6
7,2,2,1,4,5,4,7,5,8,7,6,7,2,2,1,4,5,4,7,5,8,7,6
3,2,6,4,7,3,8,1,9,1,7,3,3,2,6,4,7,3,8,1,9,1,7,3
7,4,3,7,5,1,9,4,5,5,9,1,7,4,3,7,5,1,9,4,5,5,9,1
6,7,4,9,8,8,7,5,6,1,7,2,6,7,4,9,8,8,7,5,6,1,7,2
1,6,7,4,6,2,9,9,6,2,3,9,1,6,7,4,6,2,9,9,6,2,3,9
4,2,2,8,6,5,9,8,6,5,1,7,4,2,2,8,6,5,9,7,5,5,1,7
3,8,1,2,7,7,7,5,7,5,3,9,3,8,1,2,7,7,7,5,7,5,3,9
6,9,2,8,2,7,6,5,6,9,1,6,6,9,2,8,2,7,6,5,6,9,1,6
8,5,8,7,8,3,3,5,1,3,6,3,8,5,8,7,8,3,2,5,1,3,6,3
9,4,5,6,9,5,8,7,8,7,5,6,9,4,5,6,9,5,8,7,8,7,5,6
8,9,6,7,9,7,9,1,6,7,9,3,8,9,6,7,9,7,9,1,6,7,9,3
5,1,4,8,2,4,1,1,9,9,1,4,5,1,4,8,2,4,1,1,9,9,1,4
3,2,5,7,5,9,3,9,3,9,1,6,3,2,5,7,5,9,3,9,3,9,1,6
6,2,9,9,9,2,9,2,9,6,7,3,6,2,9,9,9,2,9,2,9,6,7,3
2,3,2,9,2,9,9,1,7,9,9,6,2,3,2,9,2,9,9,1,7,9,9,6
3,6,2,8,6,9,7,1,6,1,1,5,3,6,2,8,6,9,7,1,6,1,1,5
7,6,8,4,9,7,6,9,7,7,9,1,7,6,8,4,9,7,6,9,7,7,9,1
1,4,9,3,5,5,9,9,5,1,1,9,1,4,9,3,5,5,9,9,5,1,1,9
1,7,2,5,5,3,4,7,7,9,2,7,1,7,2,5,5,3,4,7,7,9,2,7
9,1,5,2,1,9,4,9,1,7,9,9,9,1,5,2,1,9,4,9,1,7,9,9
1,3,6,8,7,1,8,1,6,4,9,9,1,3,6,8,7,1,8,1,6,4,9,9
2,3,5,1,6,6,3,8,8,1,2,3,2,3,5,1,6,6,3,8,8,1,2,3
3,5,4,5,5,8,1,7,1,4,4,7,3,5,4,5,5,8,1,7,1,4,4,7
5,3,9,4,4,2,8,3,8,8,4,7,5,3,9,4,4,2,8,3,8,8,4,7