深度学习示例1-2

学科相关 机器学习
1

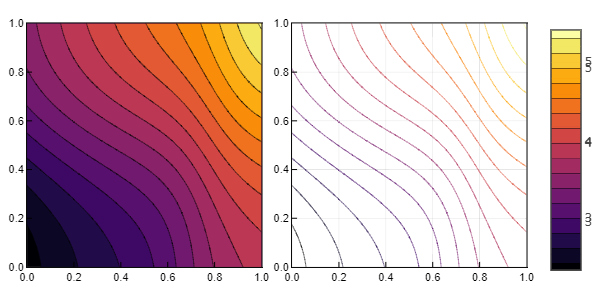
问题描述：f(x,y)=e^x+e^y 数据集选取0<x<1,0<y<1。

# ----------(x, y) -> f(x,y)--------------
using Flux;
using Flux: @epochs;

# 产生数据集
x = rand(2, 100);
f = sum(exp.(x), dims=1);
f .+= 0.5.*rand(1, length(f));
dataset = [(x, f)]; # or dataset = Iterators.repeated((x, f), 1000)

# 定义模型
m = Chain(Dense(2, 30, tanh),
    Dense(30, 20, tanh),
    Dense(20, 1));


loss(x, f) = Flux.mse(m(x), f); # 定义误差函数
opt = ADAM();
ps = params(m);

# 训练模型
for i in 1:10000
    Flux.train!(loss, ps, dataset, opt);
    if i%1000 == 0
        println("第$(i)步的误差是$(loss(x, f))");
    end
end

# # 相当于@epochs 1000 Flux.train!(loss, ps, dataset, opt, cb = throttle(evalcb, 10));
# dataset = Iterators.repeated((x, f), 10000)
# for (x, f) in dataset
#     gs = Tracker.gradient(()->@show(loss(x, f)), ps, nest=true);    # 误差梯度
#     Tracker.update!(opt, ps, gs);   # 更新误差梯度
# end

x0 = [0.5, 0.5];
println("真实值：$(sum(exp.(x0), dims=1));", "预测值：$(m(x0).data)");

# 绘图
using Plots, Cairo;
plotlyjs(size=(600,300));
x = 0.0:0.02:1.0
y = 0.0:0.02:1.0
ff(x, y) = m([x, y]).data[1]
X = repeat(reshape(x, 1, :), length(y), 1)
Y = repeat(y, 1, length(x))
Z = map(ff, X, Y)
p1 = contour(x, y, Z, fill=true, framestyle=:box)
p2 = contour(x, y, Z, framestyle=:box)
p = plot(p1, p2)
savefig(p, "example7_2D.png");

输出结果图片如下：
example7_2D

3 个赞