深度学习示例2-1

学科相关 机器学习
1

首先提醒，本内容待完善。
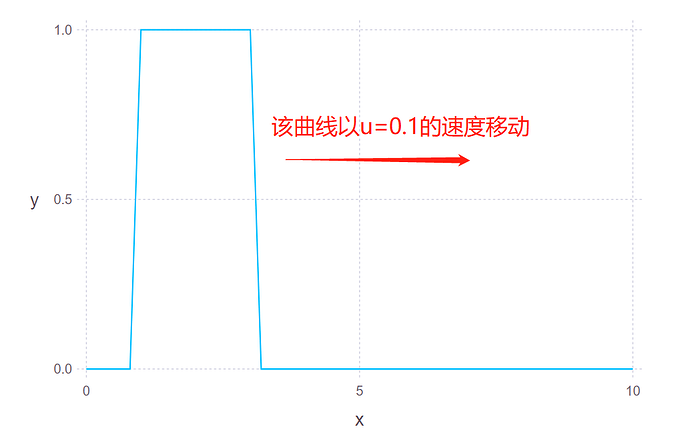
问题描述：初始值：当 0 < x < 1 ，y=0; 当 1 \leq x \leq 3 ，y=1; 当 3 < x < 10，y=0; 在控制方程(对流方程) \frac{\partial y}{ \partial t} +u\frac{\partial y}{ \partial x} = 0 下变化, 其中u常数0.1。

image
image1034×661 26.2 KB

代码如下：

# 求解方波在对流方程控制下的运动
using Flux;
using Gadfly;

# 建立数据集
x = 0:0.2:10
y = [];
for xval in x
    if xval < 1.0
        append!(y, 0.0);
    elseif xval > 3.0
        append!(y, 0.0);
    else
        append!(y, 1.0);
    end
end
x = collect(reshape(x, 1, :));
y = collect(reshape(Float64.(y), 1, :));
dataset = [(x, y)];

# 定义模型
m = Chain(Dense(1, 20, tanh),
    Dense(20, 15, tanh),
    Dense(15, 1));
ps = params(m);

loss(x, y) = Flux.mse(m(x), y); # 定义误差函数
opt = Descent(0.1);

for t in 1:3500
    println("t = $(t)");
    dataset = [(x, y)];
    # 训练模型
    for i in 1:10000
        Flux.train!(loss, ps, dataset, opt);
        if i%2000 == 0
            println("第$(i)步的误差是$(loss(x, y))。");
        end
    end
    dy(x) = Tracker.forward(m, x)[2](1)[1].data;
    y .-=  0.10 .* 0.10 .* dy(x);
    if t%10 == 0
        layer1 = Gadfly.layer(x=[1.0+0.01*t, 3.0+0.01*t], y=[1.0, 1.0], Geom.point, Theme(default_color="black"));
        layer2 = Gadfly.layer(x=x, y=y, Geom.line, Theme(default_color="red", line_width=1.2pt));
        fig1 = Gadfly.plot(layer1, layer2, Guide.xlabel("x"), Guide.ylabel("y"), Guide.title("SquareWave"), Guide.manual_color_key("Legend", ["origin", "predict"], ["black", "red"]));
        fig1 |> SVG("example7_$(t).SVG");
    end
end

结果如下：
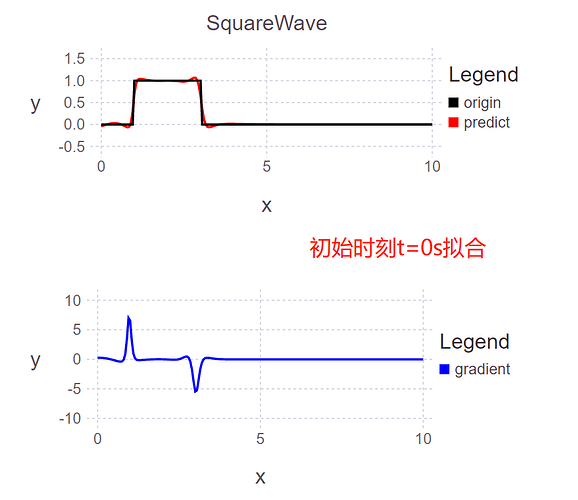
t = 0 (0.0s)

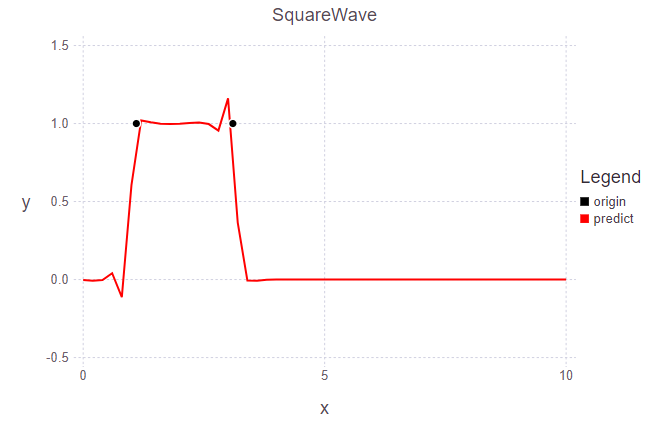
image
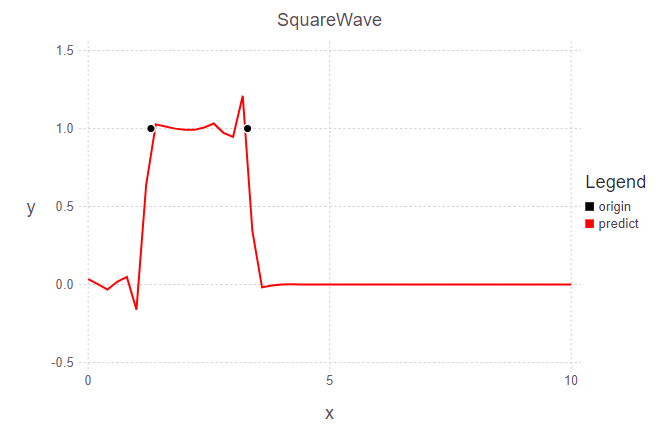
image880×760 35.1 KB

t = 10 (1.0s)

image

t = 30 (3.0s)
image

t = 100 (10.0s)
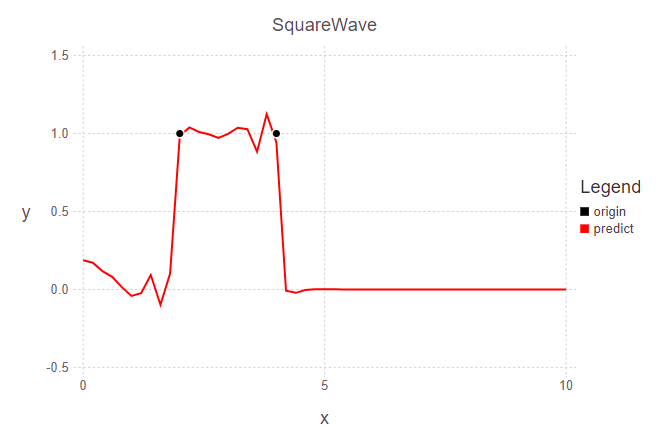
image

t = 200 (20.0s)
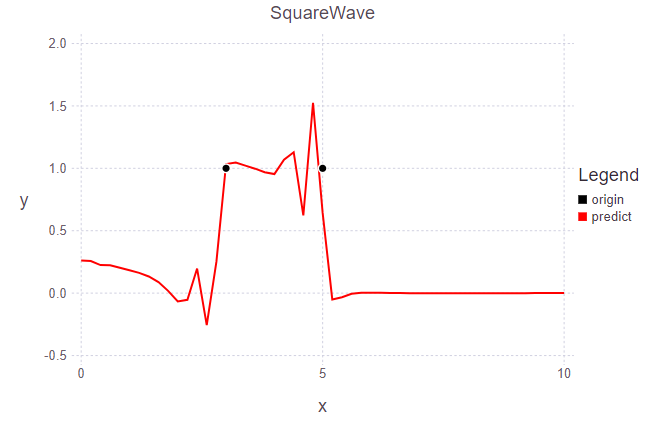
image

t = 300 (30.0s)
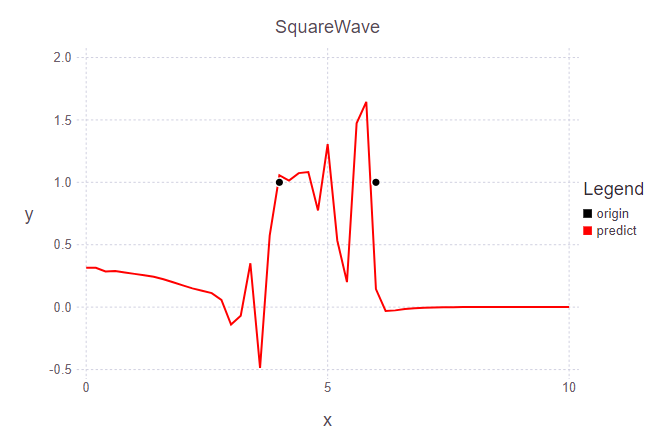
image

不足：1、神经网络结构和参数未细细调节； 2、图片未输出gif动图；3、物理参数未调节，比如数据点个数，时间步长，边界处的导数（增加曲线两端的数据点）等等；其它暂未想到。
待完善。。。。。。

2 个赞