这几天去在B站学习吴恩达老师的机器学习课程,从最简单的线性代数入手,非常有感觉,今天试着写一篇学习笔记吧,但是多媒体那些画图不怎么会,只好调最重要的讲了。
今天只模拟了一下h\theta(x)=\theta1x,
h\theta(x)=\theta0+\theta1x的情况还不会,毕竟能力有限
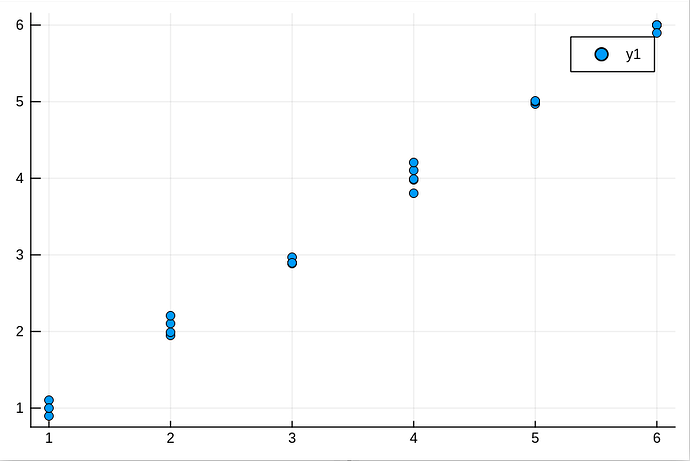
简单来说,这里需要一个假设函数来对这些点拟合,设这个假设函数为h\theta(x)=\theta0+\theta1x,为了简便,我使这些点都接近y=x这条直线,此时 \theta0=0。 并把他们保存在数据框df中,其中x=1:6,保存在L1 。L2保存对应的y值
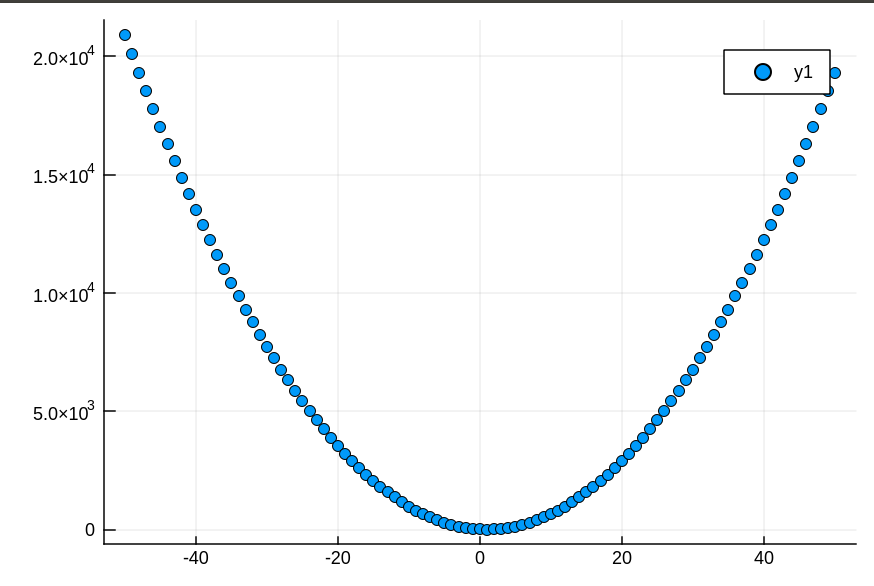
这个假设函数生成的直线拟合这些点时并不是都能和每个点拟合(其实这个名词我不太懂),所以我们引入一个代价函数J(\theta1)来表示误差。这里设J(\theta1)= 1/2m * sum( (h\theta(x(i))-y(i))2),为了计算方便,取 \theta1=-50:1:50
代价函数表示出来后需要求 \theta1,不过这个用代码写我好像不怎么会,只知道要不断更新 \theta1
\theta1 :=\theta1- \alpha * J'(\theta)(这里导数不会打)直到导数接近0
代码我写这了
import CSV
using DataFrames
using Plots
df=CSV.read("list.csv")#list.csv保存了原始的x,y数据
list=[x for x in -50:50]#这个list用来辅助下面的symbollist
symbollist=[Symbol(:D,x) for x in list]#用来命名df中的列名
for θ1 in -50:50
df[!,symbollist[θ1+51]] = df[!,:L2] * θ1 #hθ(x) = θ1*x
end
list=Vector{Float64}(undef,101)#名字一样,不过无所谓啦,这里用作代价函数
for i in -50:50
list[i+51] = sum((df[!,symbollist[i+51]] - df[!,:L2]).^2)/50
end
scatter(-50:1:50,list)
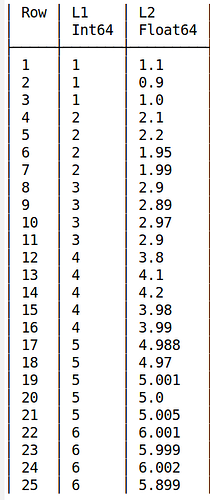
这是list.csv
L1,L2
1,1.1
1,0.9
1,1.0
2,2.1
2,2.2
2,1.95
2,1.99
3,2.9
3,2.89
3,2.97
3,2.9
4,3.8
4,4.1
4,4.2
4,3.98
4,3.99
5,4.988
5,4.97
5,5.001
5,5.0
5,5.005
6,6.001
6,5.999
6,6.002
6,5.899
另外这个更新 \theta1的代码有点不想写,有哪位能借我抄一下![]()
顺便问一下有 \theta0时这个代码逻辑是怎么样的?