请问这个代价函数的导数怎么求

[nesteiner]

有一个数据集df:

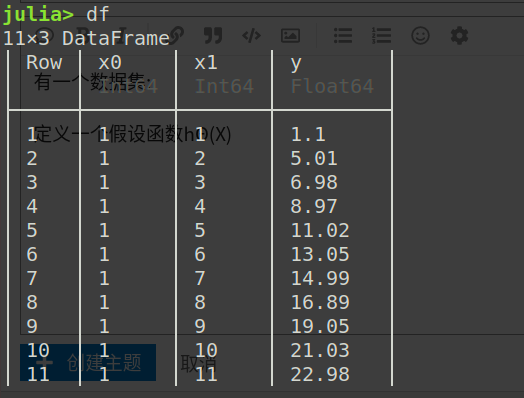
我想用函数y=2x+1对这个数据集进行拟合
定义Xⁱ为第i行的x0,x1组成的矩阵[x₀ⁱ;x₁ⁱ] x₀为1。 (竖着的,markdown语法不怎么熟悉)
Θ为矩阵[Θ₀;Θ₁] (也是竖着的)
假设函数hΘ(Xⁱ)=Θ₀+Θ₁=Θ^TX
代价函数J(Θ)=1/2m * ∑(hΘ(Xⁱ)-yⁱ)² (i=1:m)

现在请问代价函数的导数怎么用矩阵表示？？
高数还没学到那一块，有那位能教教我
ps:我在网上复制的矩阵的markdown命令怎么在这里显示不出来？？

---

好像可以这样，定义矩阵X为
|x₀ x₁¹ x₂¹ . . .x_n¹|
|x₀ x₁² x₂² . . .x_n²|
|. . . . . . . . . . . . . . |
|x₀ x₁^m x₂^m . . . x_n^m|
有m个数据集
其中Θ为
|Θ₀|
|Θ₁|
|…|
|Θ_n|
这样J(Θ)=1/2m * sum((Θ^TX-y).^2),这样就好弄多了
请问这个J(Θ)导数怎么写啊

[johnnychen94]

链式法则：

J' = \frac{m}{2}\sum_i(\frac{\partial J}{\partial X_i}) = m\sum_i[X_i(\Theta^TX_i - Y_i)]

[KBits_PenPen]

可以记 x= \begin{bmatrix} x_{01} &x_{02}&\cdots&x_{0m}\\ x_{11} &x_{12}&\cdots&x_{1m} \end{bmatrix},

y= \begin{bmatrix} y_{1} &y_{2}&\cdots& y_{m} \end{bmatrix},
\theta ^T= \begin{bmatrix} \theta_{1} &\theta_{2} \end{bmatrix},
则 y=\theta^T x.
J(\theta)=\frac{1}{2m}(y-\theta^T x)^2

则导数 \frac{\partial{J}}{\partial{\theta}}= -\frac{1}{m}(y-\theta^T x)x^T ，和 \theta 维度是一致的。
打公式的代码如下，在$号与汉字标点之间加空格就可以显示公式。

可以记

x= \begin{bmatrix} x_{01} &x_{02}&\cdots&x_{0m}\\ x_{11} &x_{12}&\cdots&x_{1m} \end{bmatrix}

y= \begin{bmatrix} y_{1} &y_{2}&\cdots& y_{m} \end{bmatrix}

\theta ^T= \begin{bmatrix} \theta_{1} &\theta_{2} \end{bmatrix}

则 y=\theta^T x .
J(\theta)=\frac{1}{2m}(y-\theta^T x)^2 则导数 \frac{\partial{J}}{\partial{\theta}}= -\frac{1}{m}(y-\theta^T x)x^T ，和 \theta 维度是一致的。

[nesteiner]

你要不把这些公式做成png再发送过来，这边显示不了

[KBits_PenPen]

看来不加空格也行，设备问题。。。