我又在github上提了一份这个问题,不知道这个机率出现得大不大
浮点数精度问题,不是语言问题
你认为错在哪里?
有小数是浮点数的精度问题。
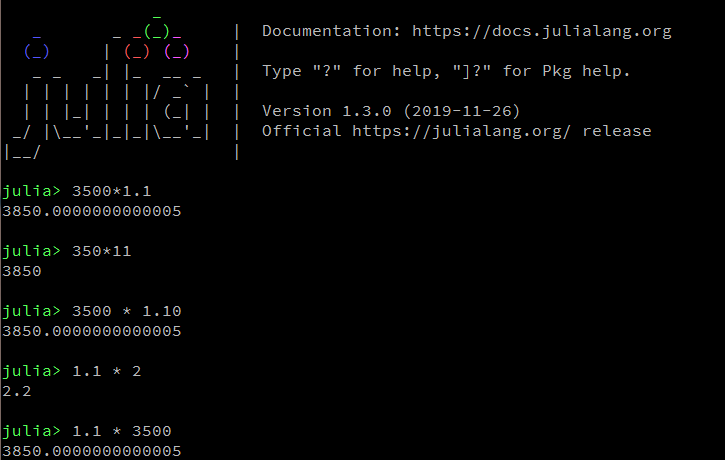
julia> 1.1*3500
3850.0000000000005
julia> eps(1.1*3500)
4.547473508864641e-13
要精确请用 BigFloat
help?> BigFloat
search: BigFloat
BigFloat <: AbstractFloat
Arbitrary precision floating point number type.
────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
BigFloat(x::Union{Real, AbstractString} [, rounding::RoundingMode=rounding(BigFloat)]; [precision::Integer=precision(BigFloat)])
Create an arbitrary precision floating point number from x, with precision precision. The rounding argument
specifies the direction in which the result should be rounded if the conversion cannot be done exactly. If not
provided, these are set by the current global values.
BigFloat(x::Real) is the same as convert(BigFloat,x), except if x itself is already BigFloat, in which case it will
return a value with the precision set to the current global precision; convert will always return x.
BigFloat(x::AbstractString) is identical to parse. This is provided for convenience since decimal literals are
converted to Float64 when parsed, so BigFloat(2.1) may not yield what you expect.
│ Julia 1.1
│
│ precision as a keyword argument requires at least Julia 1.1. In Julia 1.0 precision is the second
│ positional argument (BigFloat(x, precision)).
Examples
≡≡≡≡≡≡≡≡≡≡
julia> BigFloat(2.1) # 2.1 here is a Float64
2.100000000000000088817841970012523233890533447265625
julia> BigFloat("2.1") # the closest BigFloat to 2.1
2.099999999999999999999999999999999999999999999999999999999999999999999999999986
julia> BigFloat("2.1", RoundUp)
2.100000000000000000000000000000000000000000000000000000000000000000000000000021
julia> BigFloat("2.1", RoundUp, precision=128)
2.100000000000000000000000000000000000007
我不认为 3850 等于 3850.0000000000005
好吧,这种现像我还是很少碰到,想问下如果用小数,那要怎么样才能没有精度问题。
你用其他语言“没有碰到”只是因为它们默认打印的浮点数有效数字比较少而已。计算机无法使用浮点数精确地表示任意小数。比如,0.1。
julia> using Printf
julia> @printf("%.20f\n",0.1)
0.10000000000000000555
大家都是IEEE754,没什么错不错的。
这也就是为什么不能用==来直接比较两个浮点数。
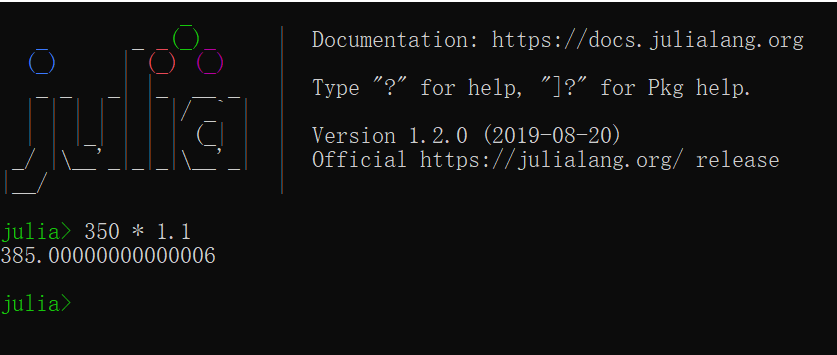
是都用的ieee这个,但处理不一样,我用别的语言 3500 * 1.1得出的是 3850 这个值,而我想要的也是3850这个值,在计算机里面3850是能正常表示的。并且就你说的错不错的问题在数学里面你那个值就是错的,这哪只能算是个近似值,你不能说没算错。
最终结果可以精确表示不能推出计算过程没有精度损失。
#include <iostream>
int main() {
std::cout << (3500.0*1.1 == 3850.0) << std::endl;
}
这是C++,结果仍然是不等于3850的
BigFloat 不会算错。
可能是它内部的表示方式不一样。
还有一个错误你没有发现 ,一个正数在很多次加一之后会变成负数。
你觉得这个也是错误吗?
近似值好歹能用,负数可怎么用啊。
我发现你是真的能扯,一个算错了的东西硬要洗成没算错,官方都承认因为数据存储的问题会造成误差,到你们这就成了没算错了。
我以前浮点计算用得不多,并没碰到过这类问题,没想到这个是因为计算机原理造成的。
这是精度问题,不是单个语言的问题,涉及到计算机底层如何处理浮点数的机制,所有语言都是一样的,甚至你打开 Windows 自带的计算器也是一样的,它们都面临同样的计算机底层处理浮点数问题,只是呈现给你看的结果不一样而已。现在大多数编程语言都遵循 IEEE 标准,举个栗子,比如单精度浮点数,底层储存一般是 32 位,比如 0.1 这个浮点数转化成二进制储存时,是个无限循环小数,但是它却又只能存储32位,所以多出来的那些只好截断,这样就有误差了,这就是为什么浮点数有时候运算完毕转化成十进制打印到屏幕时就会跟我们数学计算的结果不一样。有兴趣可以去了解计算机底层原理。