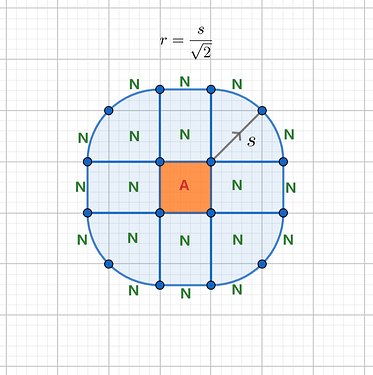
问题描述:在二维平面的一系列点中找出所有距离小于给定值s的点对,并输出结果
实现方法:
- 两重for循环 for i = 1:NumberNod-1 for j = i+1:NumerNod
- Cell List算法: 先将点放进cell中,然后只需要搜索一个邻近的8个cell即可
遇到困难:采用Cell List算法写出的代码反而没有两重for循环快
代码:
fixed-radius nearest neighbor
=============================================================================
#cell list algorithm
function FRNNMain(NumNod::Int64,Dim::Int64,A::Array{Float64,2},s::Float64)
r = s/sqrt(Dim)
PoiPair = Array{Tuple{Int64,Int64},1}(undef,1)
Cell = PoiCell(A,NumNod,r)
for key in keys(Cell)
vaule = Cell[key]
InnerCellPair!(vaule,PoiPair)
LoopNeighbor!(key,Cell,PoiPair,A,s)
end
return PoiPair
end
function PoiCell(A::Matrix{Float64},NumNod::Int64,r::Float64)
Cell = Dict()
for i = 1:1:NumNod
x = Int(floor(A[i,1]/r))
y = Int(floor(A[i,2]/r))
z = (x,y)
if z ∉ keys(Cell)
Cell[z] = [i]
else
push!(Cell[z],i)
end
end
return Cell
end
function GetNeighborCell(key::Tuple{Int64,Int64})
NeiCell = Array{Tuple}(undef,8,1)
NeiCell[1] = (key[1]+1,key[2]+1)
NeiCell[2] = (key[1]+1,key[2])
NeiCell[3] = (key[1]+1,key[2]-1)
NeiCell[4] = (key[1],key[2]+1)
NeiCell[5] = (key[1],key[2]-1)
NeiCell[6] = (key[1]-1,key[2])
NeiCell[7] = (key[1]-1,key[2]+1)
NeiCell[8] = (key[1]-1,key[2]-1)
return NeiCell
end
function InnerCellPair!(value::Array{Int64},pairs::Array{Tuple{Int64,Int64},1})
Len = length(value)
if Len >= 2
for i = 1:Len-1
for j = (i+1):Len
z = (value[i],value[j])
push!(pairs,z)
end
end
end
return pairs
end
function LoopNeighbor!(key::Tuple{Int64,Int64},Cell::Dict{Any,Any},PoiPair::Array{Tuple{Int64,Int64},1},A::Array{Float64,2},s::Float64)
value = Cell[key]
NeiCell = GetNeighborCell(key)
for i = 1:8
key1 = NeiCell[i]
if key1 ∈ keys(Cell)
value1 = Cell[NeiCell[i]]
FindPair!(value,value1,PoiPair,A,s)
end
end
return PoiPair
end
function FindPair!(value,value1,PoiPair::Array{Tuple{Int64,Int64},1},A::Array{Float64,2},s::Float64)
Len1 = length(value)
Len2 = length(value1)
for i = 1:Len1
for j = 1:Len2
P1 = value[i]
P2 = value1[j]
Point1 = A[P1,:]
Point2 = A[P2,:]
Dist = Distance(Point1,Point2)
if Dist <= s^2
AddPair!(P1,P2,PoiPair)
end
end
end
return PoiPair
end
function Distance(Point1::Array{Float64,1},Point2::Array{Float64,1})
Dist = (Point1[1]-Point2[1])^2+(Point1[2]-Point2[2])^2
return Dist
end
function AddPair!(P1::Int64,P2::Int64,PoiPair::Array{Tuple{Int64,Int64},1})
pair1 = (P1,P2)
pair2 = (P2,P1)
if pair1 ∉ PoiPair
if pair2 ∉ PoiPair
push!(PoiPair,pair1)
end
end
return PoiPair
end
NumNod = 1000
Dim = 2
A = rand(NumNod,Dim)
s = 0.1;
a = FRNNMain(NumNod,Dim,A,s)
=============================================================================#forloop
NumNod = 1000
Dim = 2
A = rand(NumNod,Dim)
s = 0.1;
function forloop(A::Matrix{Float64},NumNod::Int64,s::Float64)
PoiPair = []
for i = 1:NumNod-1
for j = i+1:NumNod
Point1 = A[i,:]
Point2 = A[j,:]
Dist = (Point1[1]-Point2[1])^2+(Point1[2]-Point2[2])^2
if Dist < s
push!(PoiPair,(i,j))
end
end
end
return PoiPair
end
b = forloop(A,NumNod,s)
=============================================================================
运行时间:
@btime FRNNMain(NumNod,Dim,A,s)
142.194 ms (79608 allocations: 7.33 MiB)
@btime forloop(A,NumNod,s)
46.899 ms (1117806 allocations: 97.09 MiB)
刚刚从Matlab转过来,profiler的结果有点看不懂,就不往上贴了
可能存在的问题:在搜索邻近cell的过程中存在着重复