在Julia中直观地求解联合初级方程

weber · 2020 年7 月 14 日 02:39

转载自https://qiita.com/KeitaNakamura/items/791ce1662a7a7fa2a4ab
机翻

weber · 2020 年7 月 14 日 02:40

签名罗金

[Qiita 夏季节] 黑客 “会计” 和 “时间”！发布免费 API 提示并获取礼物转到页面

@KeitaNakamura

更新在 2017-01-13

在朱莉娅中直观地求解联合初级方程

朱莉娅联合初级方程

6

更多 than 3 年 have passed since 最后更新。

求解一阶方程

求解一阶方程的一个基本方法是一个系数矩阵AA，未知变量矢量xx，已知变量矢量bb做，做Ax=b Ax=b从形状，x=A-一bx=A-1b会得到一个解决方案。然而，当各种条件结合在一起时，制作这种形状是相当麻烦的。

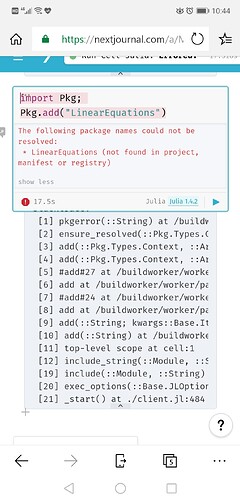
因此，我更直观地在Julia上制作了一个包，可以更直观地求解一个包和一个联合方程。

线路Equations.jl

百言一语并不像看起来那么简单，让我们立即举一个例子。

using LinearEquations sol = @linsolve x y begin x + y == 3 2x + 5y == 9 end sol # [x,y] = [2.0,1.0]

我尝试了最简单的例子。要求解方程，请使用上述宏。所需的未知变量在宏之后用 空格分隔 。表达式使用块按 换行符 排序。请注意，对于等号 **， 使用 * 而不是 *** 。它可以是一个未知变量和表达式。解由传递变量的顺序矢量获得。 @linsolve begin

左侧不需要未知变量，右侧不需要将已知变量放在一起。例如，

x, y = @linsolve x y begin 3(x - 2y) + 10 == y - 7 6x + 5y == 4 end x # -1.0 y # 2.0

也是可能的。

此外，如果你使用公式， Rational

x, y = @linsolve x y begin x + 2y == 2 -2//3*x + y == 1//2 end x # 3//7 y # 11//14

以分数的形式获得解。

使用矢量变量

变量可以使用矢量，而不仅仅是标量。在这种情况下，在声明未知变量时，将指定矢量的长度。 =>

x, y = @linsolve x=>3 y=>3 begin 2eye(3)*x == y x[2] == x[3] x[1] + x[2] + x[3] == 0.0 y[end] == 0.1 end x # [-0.1,0.05,0.05] y # [-0.2,0.1,0.1]

指定矢量元素时，可以指定矢量等。 [1,3] 1:3 1:2:5 Range end :

内部でやっていること

プログラム内でやっていることの本質は超単純です．未知変数を全て順番通りにxxベクトルに並べて，係数行列AAと既知ベクトルbbを作り，と解いているだけです．ただこの方法の場合，未知変数の数をとすると，より小さいサイズの行列で解けるような場合にも，必ずの大きさの係数行列を作らなければならないため，場合によってはかなり計算速度に効いてきます．ここらへんは，今後単純な条件の場合は，小さいサイズで解くように改良したいなと思っています． x = A \ b n n n×n A