更新1:
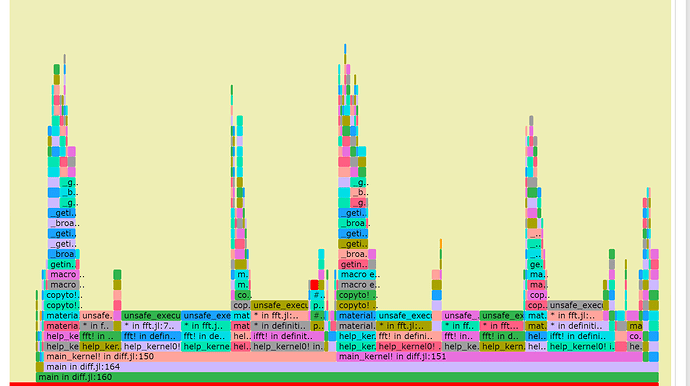
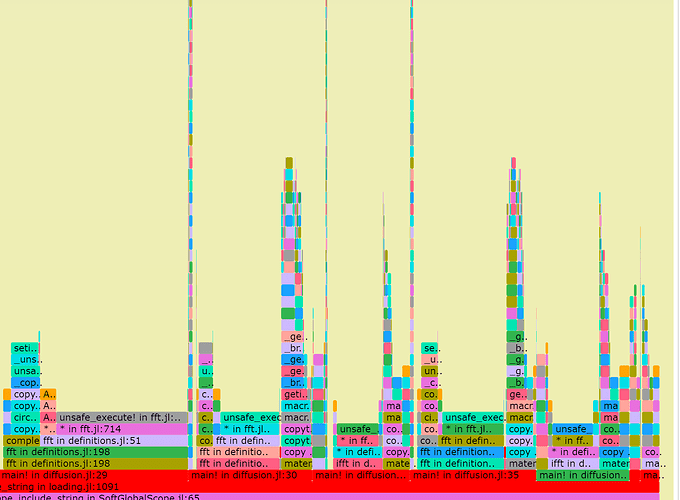
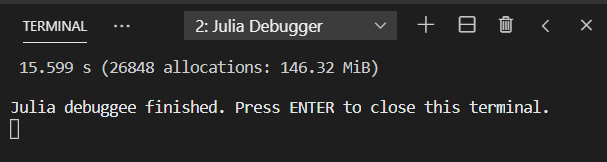
谢 woclass回复,在main!内for循环前加了三行pre-allocations(节省3s),并调用MKL,目前耗时为24s。不知还有没有进步空间?
原问题:
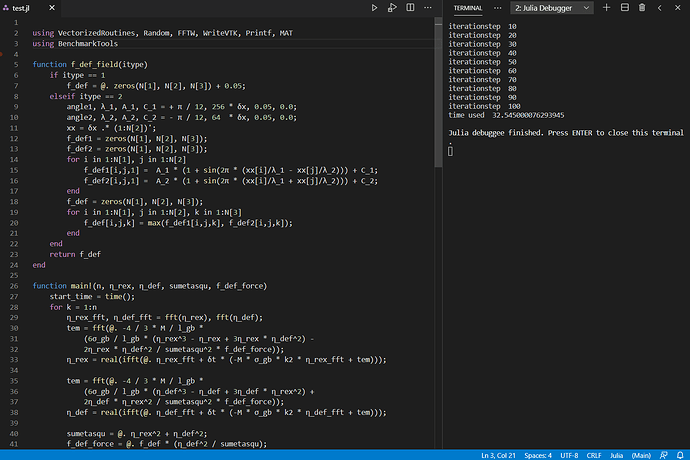
已尽己所能进行了优化,奈何经验不足,模型尺寸在 1024X1024X1 的情况下main!中的100次循环目前用时32.545s。 由于最终模型规模在5000X5000X1,且要循环100000+步,所以速度十分重要,恳请各位专家前辈予以指导优化(主要为main!中for循环),不胜感激。
using VectorizedRoutines, Random, FFTW, Printf, MAT
function f_def_field(itype)
if itype == 1
f_def = @. zeros(N[1], N[2], N[3]) + 0.05;
elseif itype == 2
angle1, λ_1, A_1, C_1 = + π / 12, 256 * δx, 0.05, 0.0;
angle2, λ_2, A_2, C_2 = - π / 12, 64 * δx, 0.05, 0.0;
xx = δx .* (1:N[2])';
f_def1 = zeros(N[1], N[2], N[3]);
f_def2 = zeros(N[1], N[2], N[3]);
for i in 1:N[1], j in 1:N[2]
f_def1[i,j,1] = A_1 * (1 + sin(2π * (xx[i]/λ_1 - xx[j]/λ_2))) + C_1;
f_def2[i,j,1] = A_2 * (1 + sin(2π * (xx[i]/λ_1 + xx[j]/λ_2))) + C_2;
end
f_def = zeros(N[1], N[2], N[3]);
for i in 1:N[1], j in 1:N[2], k in 1:N[3]
f_def[i,j,k] = max(f_def1[i,j,k], f_def2[i,j,k]);
end
end
return f_def
end
function main!(n, η_rex, η_def, sumetasqu, f_def_force)
start_time = time();
# pre-allocations
η_rex_fft = zeros(Complex{Float64}, N[1], N[2], N[3]);
η_def_fft = zeros(Complex{Float64}, N[1], N[2], N[3]);
tem = zeros(Complex{Float64}, N[1], N[2], N[3]);
for k = 1:n
η_rex_fft, η_def_fft = fft(η_rex), fft(η_def);
tem = fft(@. -4 / 3 * M / l_gb *
(6σ_gb / l_gb * (η_rex^3 - η_rex + 3η_rex * η_def^2) -
2η_rex * η_def^2 / sumetasqu^2 * f_def_force));
η_rex = real(ifft(@. η_rex_fft + δt * (-M * σ_gb * k2 * η_rex_fft + tem)));
tem = fft(@. -4 / 3 * M / l_gb *
(6σ_gb / l_gb * (η_def^3 - η_def + 3η_def * η_rex^2) +
2η_def * η_rex^2 / sumetasqu^2 * f_def_force));
η_def = real(ifft(@. η_def_fft + δt * (-M * σ_gb * k2 * η_def_fft + tem)));
sumetasqu = @. η_rex^2 + η_def^2;
f_def_force = @. f_def * (η_def^2 / sumetasqu);
if mod(k, 10) == 0
println("iterationstep ", k)
end
end
end
## 主程序
FFTW.set_num_threads(4)
const n = 100;
const N = [1024 1024 1];
const M = 1.;
const v_gb = 1.;
const δx = 1.;
const δt = 0.05;
l_gb = sqrt(9.6) * δx;
const σ_gb = 0.32;
f_def = f_def_field(2);
f_def_force = f_def;
η_rex = zeros(N[1], N[2], N[3]);
η_rex[1:5, :, :] .= 1.;
η_def = @. 1. - η_rex;
sumetasqu = @. η_rex^2 + η_def^2;
ϕ_def = @. η_def^2 / sumetasqu;
f_def_force = @. f_def_force * ϕ_def;
g = @. 2π / N[1] / δx * [ 0:N[1] / 2; -N[1] / 2 + 1:-1 ];
gg = @. 2π / N[2] / δx * [ 0:N[2] / 2; -N[2] / 2 + 1:-1 ];
ggg = @. 2π / N[3] / δx * [ 0:N[3] / 2; -N[3] / 2 + 1:-1 ];
g1, g2, g3 = Matlab.meshgrid(g, gg, ggg);
k2 = @. g1^2 + g2^2 + g3^2;
start_time = time();
main!(n, η_rex, η_def, sumetasqu, f_def_force)
println("time used ", time() - start_time)