用julia做柱壳振动计算

[Bubble]

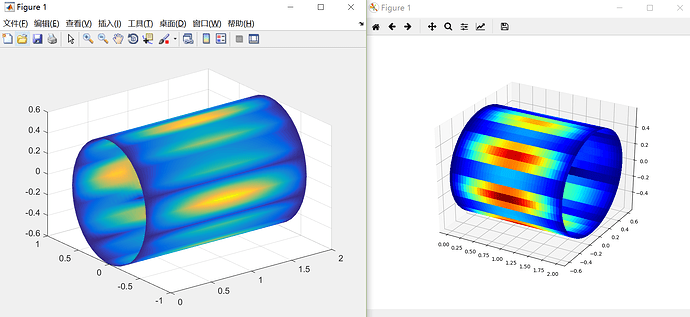
我原来用matlab做过柱壳表面振速计算，现在想转到julia上，程序写好了但运行不了。我把matlab和julia程序都放上来。matlab程序是好的，julia程序不行，有没有哪个好心人帮我改下。

首先是matlab程序

clear;clc;

omiga = 2*pi*100;      %角频率

%----------------------------------------------------
%圆柱壳体物理相关参数
r = 1.2;
a = 0.6;    %半径
L = 2;      %圆柱体长度
h = 0.006;   %壳体厚度
roup = 7800;    %壳体密度
E = 2.1e11;     %壳体杨氏模量
v = 0.3;         %泊松比
cp = sqrt(E/((1-v^2)*roup));%壳体展开为平板时的纵波速度
beta2 = h^2/(12*a^2);   %弯曲应力的作用。
%欧米咖 = omiga*a/cp;
%----------------------------------------------------
%水介质参数
rou0 = 1000;    %水密度
c = 1500;       %水中声速
k0 = omiga/c;   %波数

%----------------------------------------------------
%仿真计算参数
F0r = 1;        %激励
Z0 = L/2;
fai0 = 0;       %俯仰角
Z = 0:L/40:L;   %网格划分
fai = (0:pi/20:2*pi)';
Wz = zeros(length(fai),length(Z));
PrfaiZ = zeros(size(Wz));
alpha = 1;      %0,1对应周向的对称及非对称振动
pp = [];
mP = [];
ZA = [];
WNM = [];
zo=[];
%----------------------------------------------------
%为了避开奇点可以在奇点处加减一个微小量
di = 0.1e-5;
dp = 0.1e-5;


%----------------------------------------------------
%布传感器阵一共7*7个
% Sn.d = 0.25;%传感器间隔0.25m
% Sn.Z = 1.75:-0.25:0.25;%轴向分布
% Sn.Y = 0.75:-0.25:-0.75;%垂直方向分布
% Sn.X = -2.5;%圆柱轴线与传感器阵面的距离
% Sn.R = zeros(length(Sn.Y),length(Sn.Z));%水听器处于以圆柱轴线为中心的半径
% Sn.fai = zeros(length(Sn.Y),length(Sn.Z));%水听器与轴线和水平面形成的角度
% for i = 1:length(Sn.Y)
% 	Sn.R(i) = sqrt(Sn.Y(i)^2+Sn.X^2);
% 	Sn.fai(i) = atan2(Sn.X,Sn.Y(i));
% end
% PrfaiZ = zeros(length(Sn.Y),length(Sn.Z));


%----------------------------------------------------
% for alpha = 0:1,因为是中心起振，所以可以屏蔽
for n = 0:20
    for m = 1:30
        
        km = m*pi/L;    %轴向波数
        if n ==0 
            ita = 1;
        else
            ita = 2;
        end
        Falphanmr = ita/(pi*a*L)*F0r*sin(n*fai0+alpha*pi/2)*sin(km*Z0);  %法向激励
        
% %--------------------------------------------------------------------------------------------------------------------------
%         %上交博士论文中的声阻抗，这个阻抗公式忽略了互阻抗，在低于190Hz时计算的位移分布和comsol能完全一致，在低于170Hz情况下大小和位移分布都和comsol一致
        wight = 1j*8*pi*m^2/(k0*L)^3*rou0*c;
        mdeta = mod(m,2);
        %下面要真对x>1和x<1分段
        if n == 0
            Zh = @(x)sin(x*L*k0/2+mdeta*pi/2).^2./((km/k0)^2-x.^2).^2.*besselh(0,sqrt(1-x.^2)*k0*a)./(-1*besselh(1,sqrt(1-x.^2)*k0*a))./sqrt(1-x.^2);
            Zk = @(x)sin(x*L*k0/2+mdeta*pi/2).^2./((km/k0)^2-x.^2).^2.*besselk(0,sqrt(x.^2-1)*k0*a)./(-besselk(1,sqrt(x.^2-1)*k0*a))./sqrt(x.^2-1);
        else
            Zh = @(x)2*sin(x*L*k0/2+mdeta*pi/2).^2./((km/k0)^2-x.^2).^2.*besselh(n,sqrt(1-x.^2)*k0*a)./(besselh(n-1,sqrt(1-x.^2)*k0*a)-besselh(n+1,sqrt(1-x.^2)*k0*a))./sqrt(1-x.^2);
            Zk = @(x)2*sin(x*L*k0/2+mdeta*pi/2).^2./((km/k0)^2-x.^2).^2.*besselk(n,sqrt(x.^2-1)*k0*a)./(besselk(n-1,sqrt(x.^2-1)*k0*a)-besselk(n+1,sqrt(x.^2-1)*k0*a))./sqrt(x.^2-1);
        end
        %针对k0>km,和k0<km积分要分三段，k0<km:(0,1)(1,km/k0)(km/k0,100).k0>km:(0,km/k0)(km/k0,1)(1,100)
        if k0<km
            Znmm = wight*(quadgk(Zh,0,1-di)+quadgk(Zk,1+di,km/k0-di)+quadgk(Zk,km/k0+di,100));
        else
            Znmm = wight*(quadgk(Zh,0,km/k0-di)+quadgk(Zh,km/k0+di,1-di)+quadgk(Zk,1+di,100));
        end

%------------------------------------------------------------------------------

%下面是弗留格函数,结果比上交的唐纳尔好很多，可能是上交论文中的唐纳尔方程不太对
        S11 = -(km)^2-(1+beta2)*(1-v)*n^2/2/a^2+omiga^2/cp^2;
        S12 = -(1+v)/2*km*n/a;
        S13 = km*v/a+beta2*(a*km^3-(1-v)/2*km*n^2/a);
        S21 = S12;
        S22 = -(1+3*beta2)*(1-v)/2*km^2-n^2/a^2+omiga^2/cp^2;
        S23 = n/a^2+beta2*km^2*n*(3-v)/2;
        S31 = -S13;
        S32 = -S23;
        S33 = 1/a^2+beta2*(km^2*a+n^2/a)^2+beta2*(1-2*n^2)/a^2-omiga^2/cp^2-1j*omiga*(1-v.^2)/(E*h)*Znmm;
        SS = [S11 S12 S13;S21 S22 S23;S31 S32 S33];
        SB = [S11 S12 0;S21 S22 0;S31 S32 (1-v.^2)/(E*h)*Falphanmr];%1./(roup*cp^2*h) (1-v.^2)/(E*h)*
        %计算柱壳法向位移
        Walphanm = det(SB)/det(SS);
        WNM = [WNM Walphanm];
       Wz = Wz+Walphanm.*sin(n*fai+alpha*pi/2)*sin(km.*Z);

    end
end


% end
figure
[X,Y] = meshgrid(Z,fai);
surf(X,a*cos(Y),a*sin(Y),abs(Wz));
shading flat
shading interp

下面是julia程序

using SpecialFunctions
using LinearAlgebra
using QuadGK
using PyPlot
#-----------------------------------------
ω = 2*pi*100
a = 0.6
L = 2
h = 0.006
ρ = 7800
E = 2.1e11
ν = 0.3
cp = sqrt(E/((1-ν^2)*ρ))
β2 = h^2/(12*a^2)
#----------------------------------------
ρ0 = 1000
c = 1500
k0 = ω/c
F0r = 1
Z0 = L/2
ɾ0 = 0
Z = LinRange(0.0,2.0,41)
Z = Z'
ɾ = LinRange(0.0,2pi,41)

Wz = zeros(41,41)+zeros(41,41).*1im
Wαnm = 0+0im
S11 = 0+0im
S12 = 0+0im
S13 = 0+0im
S21 = 0+0im
S22 = 0+0im
S23 = 0+0im
S31 = 0+0im
S32 = 0+0im
S33 = 0+0im
SS  = zeros(3,3)+zeros(3,3).*1im
SB  = zeros(3,3)+zeros(3,3).*1im
Znmm = 0+0im
α = 1
di = 0.1e-5
dp = 0.1e-5

for n = 0:20
    for m = 1:30
 
        km = m*pi/L
        if n == 0
            η = 1
        else
            η = 2
        end
        Fαnmr = η/(pi*a*L)*F0r*sin(n*ɾ0+α*pi/2).*sin(km*Z0)
        wight = 1im*8*pi*m^2/(k0*L)^3*ρ0*c
        mdeta = mod(m,2)

        zh(x) = 2*sin(x*L*k0/2+mdeta*pi/2)^2/((km/k0)^2-x^2)*besselh(0,sqrt(1-x^2)*k0*a)/(besselh(n-1,sqrt(1-x^2)*k0*a)-besselh(n+1,sqrt(1-x^2)*k0*a))/sqrt(1-x^2)
        zk(x) = 2*sin(x*L*k0/2+mdeta*pi/2)^2/((km/k0)^2-x^2)*besselk(0,sqrt(x^2-1)*k0*a)/(besselk(n-1,sqrt(x^2-1)*k0*a)-besselk(n+1,sqrt(x^2-1)*k0*a))/sqrt(x^2-1)

        if k0<km
            Znmm = wight.*(quadgk(zh,di,1-di) +  quadgk(zk,1+di,km/k0-di))
        print(Znmm)
        else
            Znmm = wight.*(quadgk(zh, km/k0+di,1-di))
        end
        S11 = -(km)^2-(1+β2)*(1-ν)*n^2/2/a^2+ω^2/cp^2
        S12 = (1+ν)/2*km*n/a;
        S13 = km*ν/a - β2*(km^3*a-(1-ν)/2*km*n^2/a)
        S21 = S12
        S22 = -(1+3*β2)*(1-ν)/2*km^2-n^2/a^2+ω^2/cp^2
        S23 = -n/a^2-β2*km^2*n*(3-ν)/2
        S31 = -S13
        S32 = -S23
        S33 = -1/a^2-β2*(km^2+n^2/a)^2-β2*(1-2*n^2)/a^2+ω^2/cp^2+1im*ω*(1-ν^2)/(E*h)*Znmm[1]
        SS = [S11 S12 S13;S21 S22 S23;S31 S32 S33]
        SB = [S11 S12 0;S21 S22 0;S31 S32 (1-ν^2)/(E*h)*Fαnmr]
        Wαnm = det(SB)/det(SS)
        print(SB)
    end
end
cylx = sin.(ɾ)*ones(1,41)
cyly = cos.(ɾ)*ones(1,41)
cylz = abs.(Wz)
surf(cylx,cyly,cylz,rstride = 4,cstride = 4)

[Roger]

先把报错贴上来，然后用函数把你的Julia程序封装封装，一个是这样很慢，第二个是也太难读了吧。本来MATLAB就够丑了。

[Bubble]

/home/bubble/.local/lib/python3.6/site-packages/matplotlib/backends/backend_gtk3agg.py:16: UserWarning: The Gtk3Agg backend is known to not work on Python 3.x with pycairo. Try installing cairocffi.
"The Gtk3Agg backend is known to not work on Python 3.x with pycairo. "
ERROR: LoadError: MethodError: no method matching +(::Tuple{Complex{Float64},Float64}, ::Tuple{Float64,Float64})
Closest candidates are:
+(::Any, ::Any, !Matched::Any, !Matched::Any…) at operators.jl:502
+(!Matched::PyCall.PyObject, ::Any) at /home/bubble/.julia/packages/PyCall/WcrLS/src/pyoperators.jl:14
+(::Any, !Matched::PyCall.PyObject) at /home/bubble/.julia/packages/PyCall/WcrLS/src/pyoperators.jl:15
Stacktrace:
[1] top-level scope at /home/bubble/WorkSpace/cylshell.jl:62
[2] include at ./boot.jl:317 [inlined]
[3] include_relative(::Module, ::String) at ./loading.jl:1038
[4] include(::Module, ::String) at ./sysimg.jl:29
[5] exec_options(::Base.JLOptions) at ./client.jl:229
[6] _start() at ./client.jl:421
in expression starting at /home/bubble/WorkSpace/cylshell.jl:61

应该就是积分那的问题

[Roger]

Znmm = wight.*(quadgk(zh,di,1-di) +  quadgk(zk,1+di,km/k0-di))

改为

Znmm = wight.*(quadgk(zh,di,1-di) .+  quadgk(zk,1+di,km/k0-di))

或者在0.7+里有更快的fused broadcast，（看不懂查文档）

Znmm = @. wight * ($(quadgk(zh,di,1-di)) +  $(quadgk(zk,1+di,km/k0-di)))

还有你这个代码写出来绝对很慢，把该封装的都写到函数里面去，别在Julia里面写MATLAB。

[Bubble]

嗯，我知道了，谢谢。

[Roger]

纠正一个typo：wight → weight

[Roger]

我发现这个库还有deprecation没修好啊，顺手给他升级到1.0了

https://github.com/JuliaMath/QuadGK.jl/pull/28

[woclass]

@Bubble
我帮你改了改，反正是能跑了。

效果感觉还行，至于为什么看上去有马赛克就不得而知了。

照着 Performance Tips · The Julia Language 应该还可以继续改进，有性能需求就自己动手了。

改的时候我发现你 Julia 这边公式打错了，emm，我是按照 Matlab 那边的公式改的，你再检查一下。

Note:

• 只用了一次的参数，我都给塞到对应的函数中了，觉得不行还可以抢救一下。
• 另外半径不用 r 我觉得不行，就改成 r 了
• 有些符号为了好看我给弄成下标了，可直接复制着用，或者到命令行里 ? α 看一下怎么输入
• LinearAlgebra 我这边 (v0.6.4) 有点问题，注释了也能用，不注释报错
• 我还加了很多输出用于调试
• 最后，改代码+修公式没花多长时间，这个bug倒是把我坑得要死

using SpecialFunctions
#using LinearAlgebra
using QuadGK
using PyPlot

# === 辅助函数 ===

# 法向激励
function F_alpha_nmr(m, n, L, r; α=1)
    α   = 1     # 0,1 对应周向的对称及非对称振动
    ɾ0  = 0     # 俯仰角
    F0r = 1     # 激励
    Z0  = L/2
    km  = m*π/L # 轴向波数

    if n == 0
        η = 1
    else
        η = 2
    end

    return η/(π*r*L) * F0r * sin(n*ɾ0+α*π/2) .* sin(km*Z0)
end

function zh(m, n, L, k₀, r)
    km = m*π/L # 轴向波数
    mdeta = mod(m, 2)

    if n == 0
        return x ->
            sin(x*L*k₀/2 + mdeta*π/2)^2 /
                ((km/k₀)^2 - x^2)^2 *
                besselh(0, sqrt(1-x^2)*k₀*r) /
               -besselh(1, sqrt(1-x^2)*k₀*r) /
                sqrt(1-x^2)
    else
        return x ->
            2*sin(x*L*k₀/2 + mdeta*π/2)^2 /
                ((km/k₀)^2 - x^2)^2 *
                besselh(0,   sqrt(1-x^2)*k₀*r) /
               (besselh(n-1, sqrt(1-x^2)*k₀*r) - besselh(n+1, sqrt(1-x^2)*k₀*r)) /
                sqrt(1-x^2)
    end
end

function zk(m, n, L, k₀, r)
    km = m*π/L # 轴向波数
    mdeta = mod(m, 2)

    if n == 0
        return x ->
            sin(x*L*k₀/2 + mdeta*π/2)^2 /
                ((km/k₀)^2 - x^2)^2 *
                besselk(0, sqrt(x^2-1)*k₀*r) /
               -besselk(1, sqrt(x^2-1)*k₀*r) /
                sqrt(x^2-1)
    else
        return x ->
            2*sin(x*L*k₀/2 + mdeta*π/2)^2 /
                ((km/k₀)^2 - x^2)^2 *
                besselk(0,   sqrt(x^2-1)*k₀*r) /
               (besselk(n-1, sqrt(x^2-1)*k₀*r) - besselk(n+1, sqrt(x^2-1)*k₀*r)) /
                sqrt(x^2-1)
    end
end

function int_zh_zk(n, m, L, k₀, r, c)
    # 避开奇点
    di = 0.1e-5
    dp = 0.1e-5 # Not Use!
    ρ₀ = 1000   # 水密度
    km = m*π/L  # 轴向波数

    wight = (im*8*π*m^2)/((k₀*L)^3) * ρ₀ * c # 声阻抗
    #print("k₀, km, wight = ", k₀, ", ", km,", ", wight, "\n")

    if k₀ < km
        return wight * (quadgk(zh(m, n, L, k₀, r), 0, 1-di) .+
                         quadgk(zk(m, n, L, k₀, r), 1+di, km/k₀-di) .+
                         quadgk(zk(m, n, L, k₀, r), km/k₀+di, 100))[1]
    else
        return wight * (quadgk(zh(m, n, L, k₀, r), 0, km/k₀-di) .+
                         quadgk(zh(m, n, L, k₀, r), km/k₀+di, 1-di) .+
                         quadgk(zk(m, n, L, k₀, r), 1+di, 100))[1]
    end
end

function pflüger(m, n,
                    arr_S, Wz, WNM,
                    L, k₀, r, c,
                    ω, ϕ, Z; α=1) # 弗留格函数
    h = 0.006   # 壳体厚度
    E = 2.1e11  # 壳体杨氏模量
    ν = 0.3     # 泊松比
    ρ = 7800    # 壳体密度
    cp = sqrt(E/((1-ν^2)*ρ)) # 壳体展开为平板时的纵波速度
    β₂ = h^2/(12*r^2) # 弯曲应力的作用


    km = m*π/L # 轴向波数
    #print("cp, β₂, km = ", cp, ", ", β₂,", ", km, "\n")

    Fαnmr = F_alpha_nmr(m, n, L, r; α=1)
    Znmm  = int_zh_zk(n, m, L, k₀, r, c)
    #print("Fαnmr = ", Fαnmr, "\n")
    #print("Znmm = ", Znmm, "\n")

    # Matrix SS
    arr_S[1,1] = -(km)^2 -
                    (1+β₂) * (1-ν)/2 * n^2/r^2 +
                    ω^2/cp^2
    arr_S[1,2] = (1+ν)/2 * km * n/r;
    arr_S[1,3] = km*ν/r -
                    β₂ * (km^3*r-(1-ν)/2*km*n^2/r)

    arr_S[2,1] = arr_S[1,2]
    arr_S[2,2] = -(1+3*β₂) * (1-ν)/2 * km^2 -
                    n^2 / r^2 +
                    ω^2 / cp^2
    arr_S[2,3] = -n/r^2 -
                    β₂ * km^2 * n * (3-ν)/2

    arr_S[3,1] = -1 * arr_S[1,3]
    arr_S[3,2] = -1 * arr_S[2,3]
    arr_S[3,3] = 1/r^2 +
                    β₂ * (km^2+n^2/r)^2 +
                    β₂ * (1-2*n^2)/r^2 -
                    ω^2 / cp^2 -
                    im * ω * (1-ν^2)/(E*h) * Znmm

    det_SS = det(arr_S)
    #show(STDOUT, "text/plain", arr_S)
    #print("\ndet(SS) = ", det_SS, "\n")

    # Matrix det_SB
    arr_S[1,3] = 0
    arr_S[2,3] = 0
    arr_S[3,3] = (1-ν^2) / (E*h) * Fαnmr

    det_SB = det(arr_S)
    #show(STDOUT, "text/plain", arr_S)
    #print("\ndet(SB) = ", det_SB, "\n\n")

    Wαnm = det_SB/det_SS
    #print("Wαnm = ", Wαnm, "\n")
    WNM[n*30 + m] = Wαnm
    Wz_t = Wαnm .* sin.(n*ϕ + α*π/2) * sin.(km.*Z)
    #print("Wz_temp = ", Wz_t'[1:20], "\n")
    Wz .+= Wαnm .* sin.(n*ϕ + α*π/2) * sin.(km.*Z)
end

# === 辅助函数 END ===


# 主循环
function main_loop(L, k₀, r, c,
                    ω, ϕ, Z)
    arr_S = fill(0.0im, 3,  3)
    Wz    = fill(0.0im, 41, 41)
    WNM   = fill(0.0im, 1,  630)
    print("@Init: anyNaN? arr_S, Wz, WNM = ", any(isnan, arr_S),any(isnan, Wz),any(isnan, WNM), "\n")

    for n = 0:20
        for m = 1:30
            pflüger(m, n,
                    arr_S, Wz, WNM,
                    L, k₀, r, c,
                    ω, ϕ, Z)
        end
    end
    print("Wz = ", Wz'[1:10], "\n")
    print("WNM = ", WNM[1:6], "\n")
    print("@REs: anyNaN? arr_S, Wz, WNM = ", any(isnan, arr_S),any(isnan, Wz),any(isnan, WNM), "\n")
    return Wz
end


function plot_result(Wz, r, ϕ, Z) # 画图

#=     cylx = sin.(ϕ) * ones(1,41)
    cyly = cos.(ϕ) * ones(1,41)
    cylz = abs.(Wz)

    surf(cylx, cyly, cylz, rstride = 4, cstride = 4)
    show() =#

    X = ones(41, 1) * Z
    Y = ϕ * ones(1, 41)

    cylx = X
    cyly = r * cos.(Y)
    cylz = r * sin.(Y)

    colors = abs.(Wz)
    print("colors = ", colors'[1:10], "\n")
    print("maximum(colors) = ", maximum(colors), "\n")
    Ncolor = colors./maximum(colors)
    print("Ncolor = ", Ncolor'[1:10], "\n")
    PyPlot.surf(cylx, cyly, cylz,
                facecolors=get_cmap("jet").o(colors/maximum(colors)),
                linewidth=0,
                antialiased=false,
                shade=false)
end



function main()
    # 圆柱壳体物理相关参数
    ω = 2*π*100 # 角频率
    r = 0.6     # 半径
    L = 2       # 圆柱体长度

    # 水介质参数
    c  = 1500   # 水中声速
    k₀ = ω/c    # 波数

    Z  = linspace(0.0, 2.0, 41)' # 网格划分
    ϕ  = linspace(0.0, 2π, 41)

    Wz = main_loop(L, k₀, r, c,
                    ω, ϕ, Z)
    plot_result(Wz, r, ϕ, Z)
end


# 主程序入口
main()

[Bubble]

我都不知道怎么感谢你了太谢谢了