eps 函数

综合讨论区 Julia入门
1

Julia新手，版本：Julia 1.5.2
关于eps函数对下面结果，尤其是第一个不太理解。。。

# Julia >eps(1.0)/eps(0.1)
# 16.0

#julia> eps(10.0)/eps(1.0)
#8.0

#julia> eps(100.0)/eps(10.0)
#8.0

#julia> eps(1.0)/eps(0.1)
#16.0

#julia> eps(0.1)/eps(0.01)
#8.0

#julia> eps(0.5)/eps(0.1)
#8.0

#julia> eps(0.2)/eps(0.1)
#2.0

#julia> eps(0.11)/eps(0.1)
#1.0
2

不太清楚你具体哪里不理解.但是你可以看下 eps 函数的定义. eps(x) 函数应该是关于 |x| 递增的

  eps(x::AbstractFloat)

  Return the unit in last place (ulp) of x. This is the distance between consecutive representable floating point values at x. In most cases, if the distance on either side of x is different, then the larger of the two is taken, that is

  eps(x) == max(x-prevfloat(x), nextfloat(x)-x)

  The exceptions to this rule are the smallest and largest finite values (e.g. nextfloat(-Inf) and prevfloat(Inf) for Float64), which round to the smaller of the values.

  The rationale for this behavior is that eps bounds the floating point rounding error. Under the default RoundNearest rounding mode, if y is a real number and x is the nearest floating point number to y, then

  |y-x| \leq \operatorname{eps}(x)/2.
3

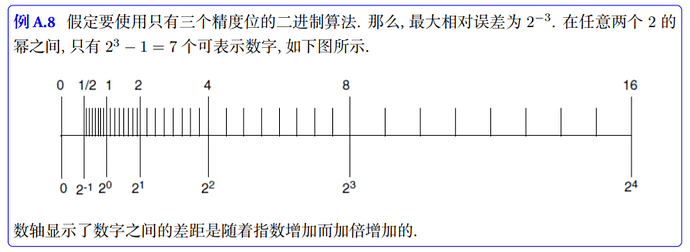
image
image895×327 69.4 KB

ref: 附录 A: IEEE 浮点运算标准

julia 中具体的计算过程

julia/float.jl at 0bedcdabeb21d0d244babb4a88c91ff75a15577f · JuliaLang/julia

eps(x::AbstractFloat) = isfinite(x) ? abs(x) >= floatmin(x) ? ldexp(eps(typeof(x)), exponent(x)) : nextfloat(zero(x)) : oftype(x, NaN)
eps(::Type{Float16}) = bitcast(Float16, 0x1400)
eps(::Type{Float32}) = bitcast(Float32, 0x34000000)
eps(::Type{Float64}) = bitcast(Float64, 0x3cb0000000000000)
eps() = eps(Float64)

# eps(x::AbstractFloat) <=> 等价于
if isfinite(x)
    if abs(x) >= floatmin(x)
        # 正常的浮点数
        ldexp(eps(typeof(x)), exponent(x))
        """
        eps(typeof(x))  取得 x 类型对应的精度常数
        exponent(x)     取得正规化浮点数 x 的指数部分
        ldexp(x, n)     计算 `x * (2^n)`
        """
    else
        # 小于 x 同类型能表示的最小的浮点数
        nextfloat(zero(x))
    end
else
    # NaN, Inf, -Inf
    oftype(x, NaN)
end
1 个赞