关于 struct, Vector 在函数中使用的疑惑

综合讨论区 语言特性及语义
1

近期在将一个 Fortran77 程序改写为 Julia，主要目的是为了学习 Julia。众所周知 Fortran77 中全局变量满天飞，给读程序和改写程序带来了很多心智负担。

为了处理这些全局变量，我把很多 common 块封装为 mutable struct 块，然后做为参数传递给 Julia 中的函数。一开始，我对所有用到 common/DataSets/ 这个块内全局变量的 Fortran 代码改写为如下代码：

mutable struct DataSets
    length
    height
    weight
end

function fun1(x::DataSets)
    y = x.length
    x.height = fun(y)
end

x = DataSets(1.0, 1.0, 1.0)
fun1(x)

我一开始修改 Fortran77 代码到 Julia 之时都是这样处理全局变量的。但是做为实参传递给函数的 DataSets 对象可以在 Julia 函数之内改变。

这就会导致如果我长时间不接触这份代码，可能必须仔细检查函数才能知道输入的参数有没有在函数内改变。 这样的代码看起来怪怪的。于是我想对在函数内修改过的结构体，返回一个新的结构体，而不对输入的参数进行修改，类似于：

function fun2(x::DataSets)
    y = x.length
    height = fun(y)
    return DataSets(x.length, height, x.weight)
end

x = DataSets(1.0, 1.0, 1.0)
fun2(x)

这样做的好处是可以一眼看出函数是否修改结构体（全局变量），但是我怀疑这样在 Julia 做是否会有性能问题？ 毕竟这里要重新构建一个 DataSets 对象。

对此我有以下问题：

  1. 我给出的两种方案，哪种是 Julia 编码规范更推荐的做法？或者说还有更优的解决方案？
  2. 对于 Julia 的 Vector 修改，我也有同样的疑惑。是修改传入的 Vector 好？还是返回一个新 Vector 更好？

谢谢！

———————————————————————————————————————
更新

我对两种方案做过简单测试，但是简单的测试代码中，两者并无明显的性能差异。

1 个赞
2

这个是编程风格的问题吧。

喜欢函数式当然就不用 mutable 的东西。
优点就是函数没有副作用，不用担心内部改了变量。
并行友好。

用 mutable 的东西好处是一次性分配内存，后面就不用多次分配。
参数、修改次数不太多的时候，性能上估计看不出太大的差别。当然还是得测试。

Vector/Array 一般来说都不小，默认就是可变的，重新分配成本较大。julia 里有很多原地修改的函数，以 ! 结尾，就是为了避免内存分配，影响性能。推荐的也是原地修改。实际上原地修改等价于 C 里传入指针。

3

感谢您非常有益的回复。

所有我感觉 Julia 在定义函数时要是能有一个类似 C/C++ 的 const Type & 这样的语法来防止修改传入的 mutable struct / Vector 该多好啊！

4

简单来说，尽可能多地使用不可变的结构体是更高效的写法。Julia 底层有非常多的优化机制，并且在实际使用上大多数时候是不会进行真正的数据复制的。例如：

struct DataSets{T}
    length::T
    height::T
    weight::T
end
Base.copy(x::DataSets) = DataSets(x.length, x.height, x.weight)

using BenchmarkTools
x = DataSets(1, 1, 1)
@btime copy($x) # 0.046 ns (0 allocations: 0 bytes)

底层的编译优化会优化掉大部分这些可能的性能开销。

用 mutable 的东西好处是一次性分配内存，后面就不用多次分配。

试图通过声明 mutable struct 来节约内存分配绝大部分时候没有意义。因为这些完全可以以更高效的矩阵或者其他的方式去实现，例如：

struct Datasets{AT<:AbstractArray}
    x::AT
    y::AT
end

实际的数据 x 和 y 依然是可变的，但是表层的结构体是不可变的。

5

关于不可变结构体最重要的一点是因为生命周期很短，大多数时候会被分配到栈内存上，因此在读取的时候效率会比较高：

mutable struct MPoint{T}
    x::T
    y::T
end

struct Point{T}
    x::T
    y::T
end

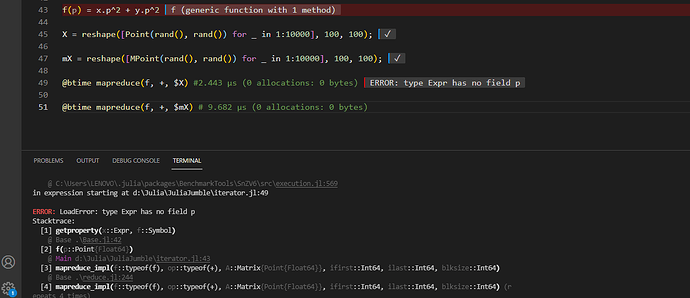
f(p) = p.x^2 + p.y^2

X = reshape([Point(rand(), rand()) for _ in 1:10000], 100, 100);

mX = reshape([MPoint(rand(), rand()) for _ in 1:10000], 100, 100);

@btime mapreduce(f, +, $X); #2.443 μs (0 allocations: 0 bytes)

@btime mapreduce(f, +, $mX); # 9.682 μs (0 allocations: 0 bytes)
1 个赞
6

请教一下，这个x 和 y 可变是从什么角度来说的，以及如何改变？能给一个简单的示例吗？非常感谢！

7 
struct MyWrapper
    data
end

X = MyWrapper(rand(4, 4))
X.data = zeros(4, 4) # 这里会报错：因为 X 是不可变的，所以不能修改 data 所指向的地址
fill!(X.data, 0) # 但是 X.data 是可变的，所以可以修改 data 所指向的地址的内容
1 个赞
8

十分抱歉，但是我复制这段代码放到vscode或repl都返回了报错。

image
image1251×542 34.3 KB

update 1

我换另一台电脑尝试运行是没问题的，但这台就是不行，跑官方文档“接口”中的第一个例子也会出现同样的报错。pkg安装包的时候也会报错，另一台电脑就不会。
我能想到两台电脑的区别在于，这台报错的电脑，在下载julia.exe的时候，只下载了个exe.
而另一台的下载下来的是一个文件夹。julia_addpkg

9

抱歉应该是 f(p) = p.x^2 + p.y^2.

10

不是很了解你那边究竟是如何操作的。有没有更具体的报错和诊断信息？这是 vscode 的问题还是 Julia 命令行的问题？你有在命令行中尝试过 Julia 么？