\begin{align}
&min\quad p+\lambda q \\
&s.t \|(z_1^{'},...,z_K^{'})\|_2^2 <= p, \quad and \quad 1'r<=q \\
&where \sqrt{\sum_{k=1}^{K}(s_i^{SV}(k))^2} <= r_i, for \quad i=1,...,N_\theta \\
&and \quad z_K=Y^{SV}(k) - As^{SV}(k), for \quad k=1,...,K.
\end{align}
不知道为什么外国论坛一直登录不上,所以没法在那上面 ![]()
hyperparameter = 2
n = size(A1, 2)
model = JuMP.Model(COSMO.Optimizer)
@variable(model, s[1:n, 1:2])
@variable(model, 0 <= p)
@variable(model, z[1:16])
@constraint(model, z .== (Ysv - A1*s)[1:end])
@constraint(model, [p; z] in SecondOrderCone())@variable(model, r[1:n] )
for i in 1:n
@constraint(model, [r[i] ; s[i, :]] in SecondOrderCone())
end
@variable(model, 0 <= q)
@constraint(model, q >= sum(r))
@objective(model, Min, p+hyperparameter * q)`
JuMP.optimize!(model)
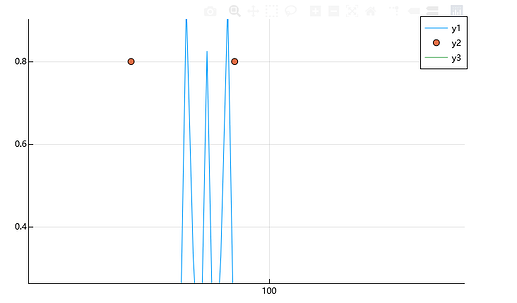
模型可以通过这样建立,建模过程建议别省步骤不然容易出错,不过我这个求出的解还不是很正确,
正确峰值应该出现在那两个点出,这里出现了三个峰值并且有一个偏离很远