有监督回归和波士顿房价预测实例

综合讨论区 心得体会
1

Table of Contents

  1. 算法介绍
    1. 基本算法
    2. l2 约束
    3. l1 约束
    4. l1 + l2 约束
  2. MLJLinearModels 使用
    1. Ridge
    2. Lasso
    3. Elastic-Net
    4. 说明
  3. 实例 波士顿房价预测
    1. 数据准备
    2. 观察各项主要特征与房价售价的关系
      1. [存疑]分析 SalePrice
      2. 分析特征数据
      3. 验证主要特征是否满足要求
      4. 主要特征
    3. 更加科学的分析数据
      1. 关系矩阵
      2. [存疑]房价关系矩阵
      3. [存疑]绘制关系点图
    4. 开始模拟数据
      1. 处理数据
      2. 模型训练
      3. 补充: lightGBM 模型训练
    5. 检验测试集数据

算法介绍

这里简要介绍下各算法和他们之间的关系，详细理解请百度一下

基本算法

最小二乘法是众多机器学习算法中极为重要的一种基础算法

单纯的最小二乘法对于包含噪声的学习过程经常有过拟合的弱点，这往往是由于学习模型对于训练样本而言过于复杂

l2 约束

由此，引入带有约束条件的最小二乘法 -— Ridge 回归

带有约束条件的最小二乘法和交叉验证法的组合，在实际应用中是非常有效的回归方法
然而，当参数特别多的时候，求解各参数以及学习得到的函数的输出值的过程，都需要耗费大量的时间

l1 约束

由此，引入可以吧大部分参数都置为0的稀疏学习算法
因为大部分参数都变成了0，所以就可以快速地求解各参数以及学习得到的函数的输出值

l1 + l2 约束

虽然 l1 约束的最小二乘学习法是非常有用的学习方法，但是在实际应用中，经常会遇到些许限制

  • 在 Lasso 回归求解路径中，对于 N×P 的设计矩阵来说，最多只能选出 min(N,p) 个变量
    当 p>N 的时候，最多只能选出N个预测变量．因此，对于 p∼N 的情况，Lasso方法不能够很好的选出真实的模型．
  • 如果预测变量具有群组效应，则用Lasso回 归时，只能选出其中的一个预测变量
  • 对于通常的 N>P 的情形，如果预测变量中 存在很强的共线性，Lasso的预测表现受控于岭回归

基于以上几点Lasso回归的局限性，Zou和 Hastie在2005年提出了弹性网回归方法，回归系 数表达式为

\hat \beta^{ridge} =\mathop{\arg\min}_{\beta} \{\sum \limits _{i=1}^{N}(y_i-\beta_0-\sum\limits_{j=1}^px_{ij}\beta_j)^2+\lambda\sum \limits_{j=1}^{p}|\beta_{j}|+\lambda\sum \limits_{j=1}^{p}\beta_{j}^2\}

MLJLinearModels 使用

Ridge

J = \frac{1}{n}\sum_{i = 1}^n (f( x_i) - y_i)^2 + \lambda \|w\|_2^2\tag{1}

RidgeRegressor

RidgeRegression()
RidgeRegression(λ; lambda, fit_intercept, penalize_intercept, scale_penalty_with_samples)

Lasso

J = \frac{1}{n}\sum_{i = 1}^n (f( x_i) - y_i)^2 + \lambda \|w\|_1\tag{2}

LassoRegressor

LassoRegression()
LassoRegression(λ; lambda, fit_intercept, penalize_intercept, scale_penalty_with_samples)

Elastic-Net

\smash{\min_{w}}\sum_{i=1}^m(y_i-\sum_{j=1}^dx_{ij}w_j)^2 + \lambda\sum_{j=1}^d|w_j|+\lambda \sum_{j=1}^dw_j^2 \tag{3}
ElasticNetRegression

ElasticNetRegression()
ElasticNetRegression(λ)
ElasticNetRegression(λ, γ; lambda, gamma, fit_intercept, penalize_intercept, scale_penalty_with_samples)

说明

其实可以不用管

  • fit_intercept
  • penalize_intercept

我也不知道这两个是干什么的，就先别管他们了
总之，只用设置 lambda 就行了

实例 波士顿房价预测

数据准备

竞赛数据来自 House Prices - Advanced Regression Techniques | Kaggle

using MLJ, CSV, StableRNGs, MLJLinearModels, Plots
import DataFrames: DataFrame, select, describe
using Statistics


dataTrain = CSV.read("data/train.csv", DataFrame)
dataTest = CSV.read("data/test.csv", DataFrame)

观察各项主要特征与房价售价的关系

[存疑]分析 SalePrice

julia> describe(dataTrain[!, :SalePrice])
Summary Stats:
Length:         1460
Missing Count:  0
Mean:           180921.195890
Minimum:        34900.000000
1st Quartile:   129975.000000
Median:         163000.000000
3rd Quartile:   214000.000000
Maximum:        755000.000000
Type:           Int64

通过上面的结果可以知道 SalePrice 没有无效或者其他非数值的数据，下面通过图示化来进一步展示 SalePrice

图片

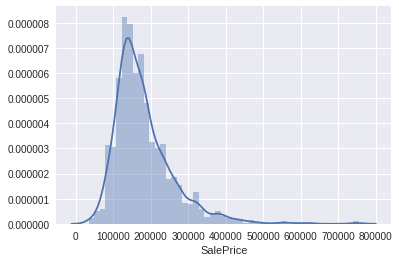
这里需要一个 distplot 函数来绘制图像

  1. 得到数组的 distribution
  2. 画出这个分布

然而我还不会这个东西，放一放

分析特征数据

入选特征

变量名 数据类型 注释
LotArea Continuous 地皮面积
GrLiveArea Continuous 生活面积
TotalBsmtSF Continuous 地下室总面积
MiscVal Continuous 其他资产
GarageCars Count 容纳车辆
GarageArea Continuous 车库面积
YearBuilt Multiclass 建造年份
CentralAir Multiclass 中央空调
OverallQual Multiclass 总体评价
Neighborhood Multiclass 地段

验证主要特征是否满足要求

  1. 类别型特征

    1. CentralAir 中央空调

      using StatsPlots
let column = :CentralAir
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    boxplot(columnX, columnY) |> display
end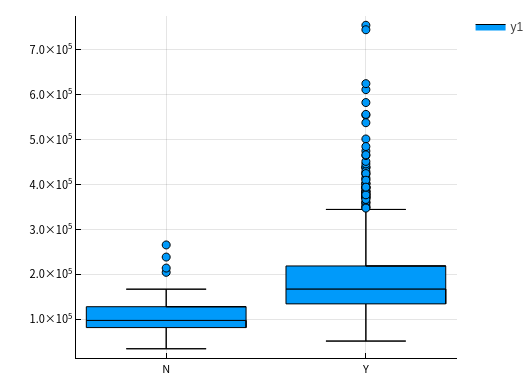

      图片

      可以很明显的看到有中央空调的房价明显更高。

    2. OverallQual 总体评价

      let column = :OverallQual
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    boxplot(columnX, columnY) |> display
end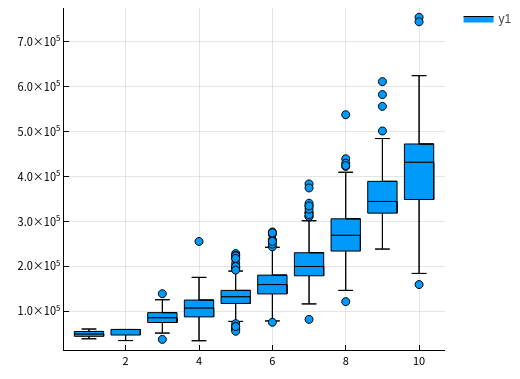

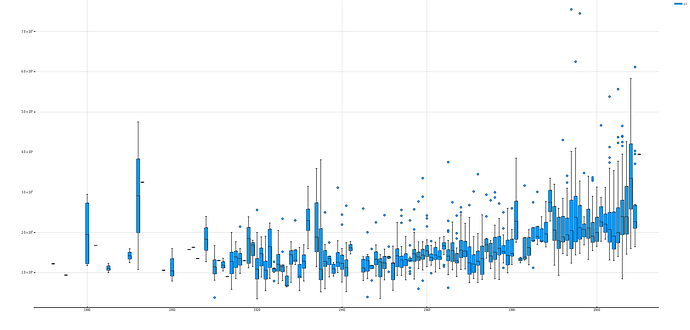
      图片

    3. YearBuilt 建造年份

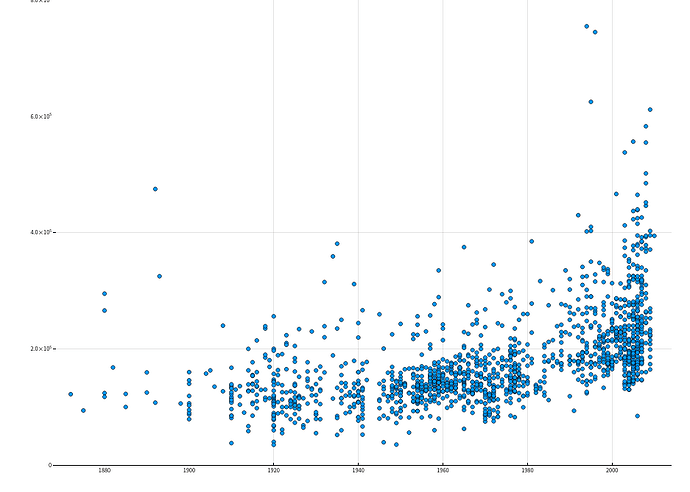
      let column = :YearBuilt
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    boxplot(columnX, columnY, size=(2600, 1200)) |> display
end

      图片
      图片1286×616 65.3 KB

      let column = :YearBuilt
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    boxplot(columnX, columnY, size=(2600, 1200)) |> display
    scatter(columnX, columnY, ylim=(0, 800000), size=(1500, 1000)) |> display
end

      图片
      图片937×669 145 KB

      最开始我是用了箱线图绘制了房价与建造年份的关系，但是并不十分明显，所以又用点图来显示，可以很明显的看到有线性增长的趋势。

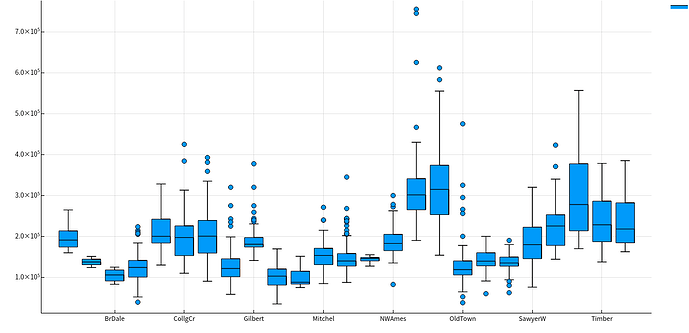
    4. Neighborhood 地段

      let column = :Neighborhood
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    boxplot(columnX, columnY, size = (1300, 600)) |> display
end

      图片
      图片1196×578 49.5 KB

      这个该怎么分析呢。。。。。。待定

  2. 数值型特征

    1. LotArea 地表面积

      let column = :LotArea
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    scatter(columnX, columnY) |> display
end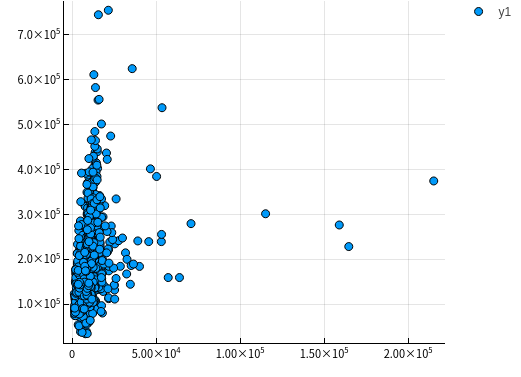

      图片

      好像该特征并没有什么差别，所以不予考虑

    2. GrLivArea 生活面积

      let column = :GrLivArea
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    scatter(columnX, columnY) |> display
end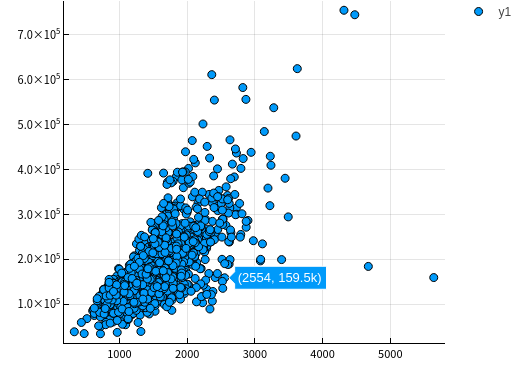

      图片

    3. TotalBsmtSF 地下室总面积

      let column = :TotalBsmtSF
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    scatter(columnX, columnY) |> display
end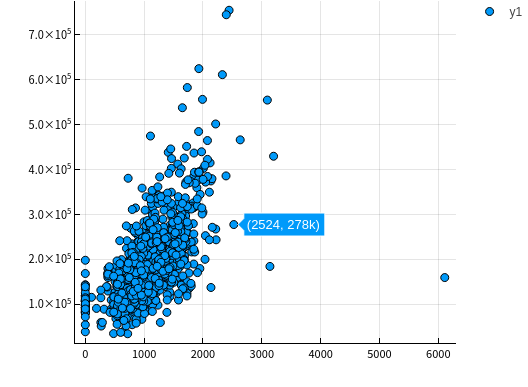

      图片

    4. MiscVal

      let column = :MiscVal
    columnY = dataTrain[!, :SalePrice]
    columnX = dataTrain[!, column]
    scatter(columnX, columnY) |> display
end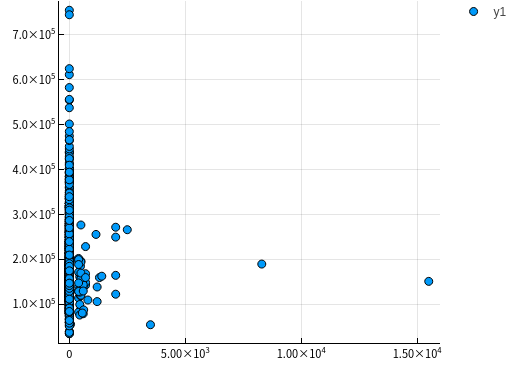

      图片

    5. GarageArea/GarageCars 车库

      let columns = [:GarageArea, :GarageCars]
    columnY = dataTrain[!, :SalePrice]
    columnXs = map(column -> dataTrain[!, column], columns)

    for columnX in columnXs
	scatter(columnX, columnY) |> display
    end
end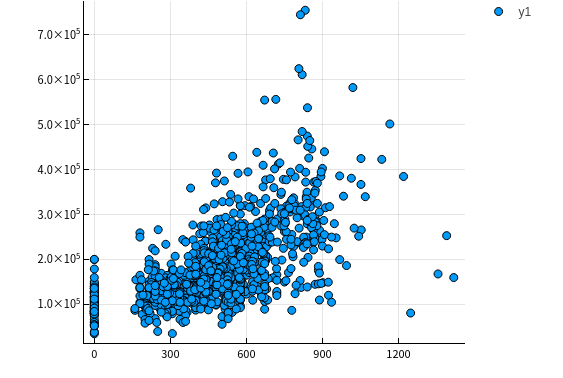

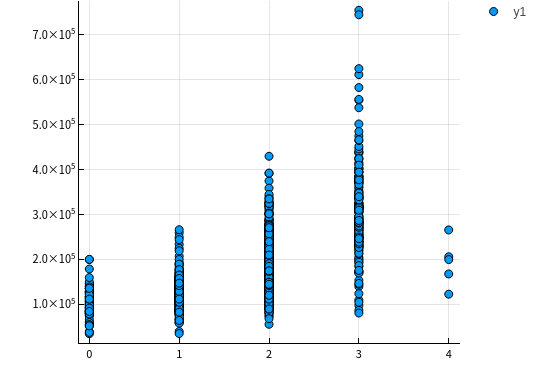
      图片

      图片

      由上面点图可以看出房价与车库面积和容纳车辆数呈现线性关系，所以入选主要特征

主要特征

总结起来，最后

变量名 数据类型 注释
GrLiveArea Continuous 生活面积
TotalBsmtSF Continuous 地下室总面积
GarageCars Count 容纳车辆
GarageArea Continuous 车库面积
YearBuilt Multiclass 建造年份
CentralAir Multiclass 中央空调
OverallQual Multiclass 总体评价
Neighborhood Multiclass 地段

更加科学的分析数据

上面的分析可以说非常主观，所以说多多少少还是会不放心，会担心自己选择的特征会不会多了或者少了，
又或者选了一些没有太大作用的特征，所以接下来需要进行更加科学的分析
为了做到更加科学，我们需要作如下工作：

  • 得到各个特征之间的关系矩阵 – correlation matrix
  • SalePrice 的关系矩阵
  • 绘制出最相关的特征之间的关系图

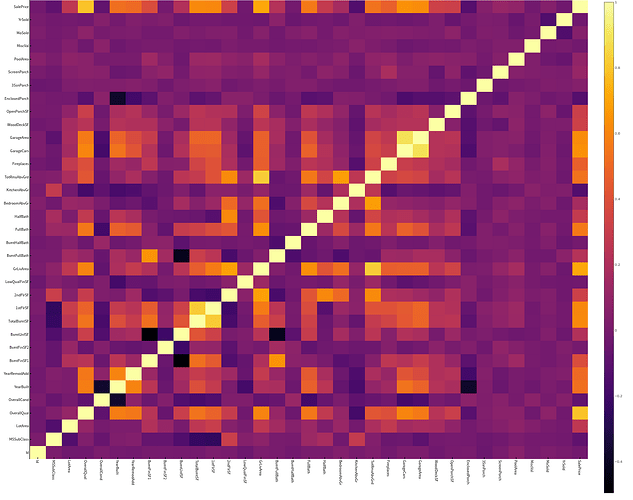
关系矩阵

教程中有局限性， 关系矩阵只涉及到数值型数据 ，这里我们也这样做，因为他的特征数有80多个，我懒得弄

let _schema = schema(dataTrain)
    _names = _schema.names
    _scitypes = _schema.scitypes
    indexs = collect(map(x -> x == Count || x == Continuous, _scitypes))
    columns = _names[indexs] |> collect
    _data = select(dataTrain, columns)
    _corr = cor(Matrix(_data))
    labels = string.(columns)
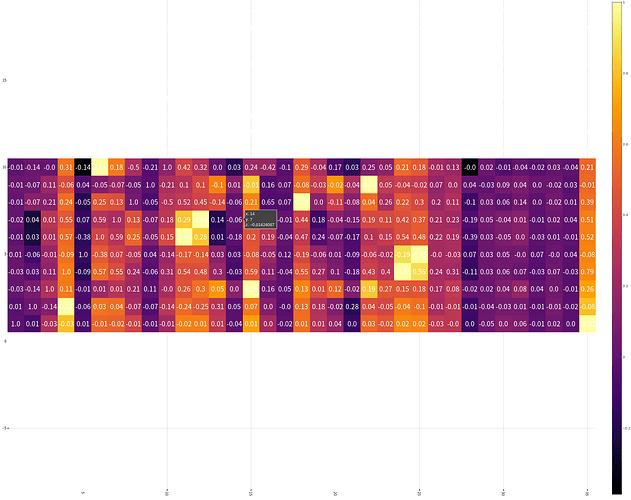
    heatmap(labels, labels, _corr, xrotation = -90, size = figureSize, xticks = :all, yticks = :all) |> display
end

图片
图片1332×1051 150 KB

像素块越亮表示两者之间相关性越强，我们可以很清楚地看到与“SalePrice”相关性很强的有

  • OverallQual 总评价
  • YearBuilt 建造年份
  • ToatlBsmtSF 地下室面积
  • 1stFlrSF 一楼面积
  • GrLiveArea 生活区面积
  • FullBath 浴室？what。。。到底什么意思，知道的麻烦说一下
  • TotRmsAbvGrd 总房间数（不包括浴室）
  • GarageCars 车库可容纳车辆数
  • GarageArea 车库面积

[存疑]房价关系矩阵

这里显示相关性最大的10个特征

k  = 10 # 关系矩阵中将显示10个特征
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(data_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, \
		 square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

我不知道这个代码是怎么运行的，他是怎么画出这个热力图的

图片

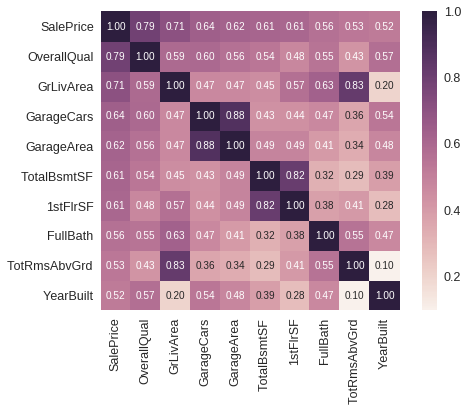
重点是 corrmat.nlargestk 是怎么得出 10x10 的矩阵

我只做到这里

let _schema = schema(dataTrain)
    _names = _schema.names
    _scitypes = _schema.scitypes
    indexs = collect(map(x -> x == Count || x == Continuous, _scitypes))
    columns = _names[indexs] |> collect
    labels = string.(columns)
    _data = select(dataTrain, columns)
    _corr = cor(Matrix(_data))

    _dataframe = DataFrame(_corr, columns)
    nlarget = _dataframe[partialsortperm(_dataframe[!, :SalePrice], 1:10, rev=true), :]

    heatmap(Matrix(nlarget), xrotation = -90, size = figureSize, xticks = :all, yticks = :all, aspect_ratio = :equal)

    nrow, ncol = size(_corr)
    fontsize = 15

    fn(tuple) = (tuple[1], tuple[2], text(round(_corr[tuple[1], tuple[2]], digits = 2), fontsize, :white, :center))
    ann = map(fn, Iterators.product(1:nrow, 1:ncol) |> collect |> vec)

    annotate!(ann, linecolor = :white) |> display
end

图片
图片1323×1048 261 KB

疑点如下

  1. 如何获取 Dataframe 最大的 10x10 切片
  2. Dataframe 的字段名也要根据数据排序进行修改吧？

[存疑]绘制关系点图

目前找到一个 PairPlots 包，我还要研究一下

开始模拟数据

处理数据

  1. 首先我们选取特征

    columns = [:OverallQual, :GrLivArea, :GarageCars, :TotalBsmtSF, :FullBath, :TotRmsAbvGrd, :YearBuilt]

  2. 定义训练集的处理模型

    trainTransformModel = Pipeline(
    FeatureSelector(features = columns),
    dataframe -> coerce(dataframe, Count => Continuous))

  3. 定义测试集的处理模型

    processFeature!(dataframe::DataFrame) = begin
    dataframe[!, :GarageCars] = replace(dataframe[!, :GarageCars], "NA" => missing)
    dataframe[!, :GarageCars] = map(x -> ismissing(x) ? x : parse(Float64, x), dataframe[!, :GarageCars])
    dataframe[!, :TotalBsmtSF] = replace(dataframe[!, :TotalBsmtSF], "NA" => missing)
    dataframe[!, :TotalBsmtSF] = map(x -> ismissing(x) ? x : parse(Float64, x), dataframe[!, :TotalBsmtSF])

    coerce!(dataframe, Count => Continuous)
    return dataframe
end

testTransformModel = Pipeline(
    FeatureSelector(features = columns),
    processFeature!,
    FillImputer(features = columns),
    # Standardizer(features = columns)
)

  4. 处理原始数据，产出数据集

    trainTransformMach = machine(trainTransformModel, dataTrain)
testTransformMach = machine(testTransformModel, dataTest)
fit!(trainTransformMach)
fit!(testTransformMach)

transformedDataTrain = transform(trainTransformMach, dataTrain)
transformedDataTest = transform(testTransformMach, dataTest)

  5. 拿出训练用数据

    X = transformedDataTrain
y = coerce(dataTrain[!, :SalePrice], Continuous)
train, test = partition(eachindex(y), 0.8, rng=rng)

模型训练

这里我们使用 Ridge 模型来检验

rng = StableRNG(1234)
cv = CV(nfolds = 6, rng = rng)
tuning = Grid(resolution=10, rng = rng)

# MODULE try Ridge
ridge = RidgeRegressor()
rangeLambda = range(ridge, :lambda, lower = 0.1, upper = 10.0, scale=:log)


tunedModel = TunedModel(model = ridge,
			range = [rangeLambda],
			measure = rms,
			resampling = cv,
			tuning = tuning)
tunedMach = machine(tunedModel, X, y)
fit!(tunedMach, rows = train)

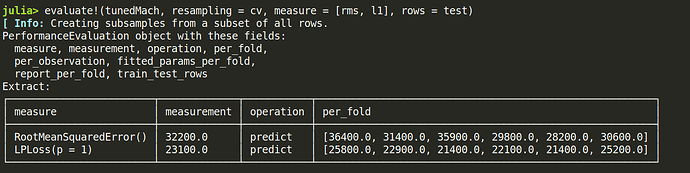
evaluate!(tunedMach, resampling = cv, measure = [rms, l1], rows = test)

图片
图片1256×315 68.5 KB

补充: lightGBM 模型训练

LGBMRegressor = @load LGBMRegressor
lgb = LGBMRegressor()
lgbm = machine(lgb, X, y)
boostRange = range(lgb, :num_iterations, lower = 2, upper = 500)
rangeLeaf = range(lgb, :min_data_in_leaf, lower = 1, upper = 50)
rangeIteration = range(lgb, :num_iterations, lower = 50, upper = 100)
rangeMinData = range(lgb, :min_data_in_leaf, lower = 2, upper = 10)
rangeLearningRate = range(lgb, :learning_rate, lower = 0.1, upper = 1)

tunedModel = TunedModel(model = lgb,
			tuning = Grid(resolution = 5, rng = rng),
			resampling = cv,
			ranges = [rangeIteration, rangeMinData, rangeLearningRate],
			measure = rms)

tunedMachine = machine(tunedModel, X, y)
fit!(tunedMachine, rows = train)
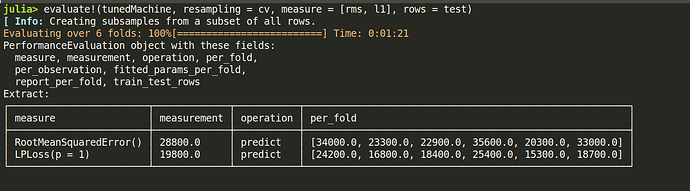
evaluate!(tunedMach, resampling = cv, measure = [rms, l1], rows = test)

图片
图片1310×363 78 KB

检验测试集数据

这里我们用 lightGBM 产出的数据来提交，不得不说，这个模型老牛逼了

predictions = predict(tunedMachine, transformedDataTest)
output = DataFrame(Id=dataTest.Id)
output[!, :SalePrice] = predictions
CSV.write("data/submission.csv", output)

图片
图片1077×175 23.4 KB

哟系

3 个赞
2

这两个的图我觉得是说明有异常值。