[DifferentialEquations.jl] ODEProblem 笔记

[nesteiner]

ODEProblem 常微分问题

介绍

对于变量 u 和 变量 t ，他们之间有关系

\frac{du}{dt} = f(u, p, t)

这其中 p 表示其他常数项系数，比如在方程

\frac{dN}{dt} = rN \left(1 - \frac{N}{K} \right)

中，p 可以为一个数组，分别表示 r 和 K

f函数参数的顺序不要搞错

描述问题

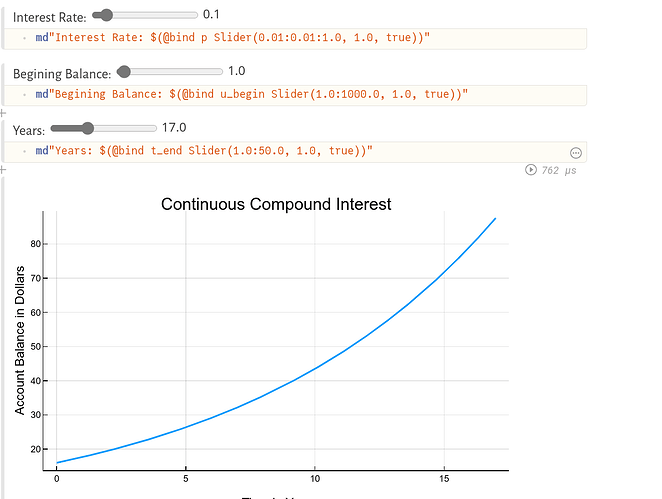
这里我们以银行复利为例，对于存款 u 与 时间 t 之间有

\frac{du}{dt} = pu

的关系
我们定义函数

f(u, p, t) = pu

我们设置

• tspan 时间范围是 (0.0, 17.0)， 表示 0 - 17年之内
• p 为 0.1 表示存款的利率
• u_begin 为 1.0 表示 t = 0 时的存款数

然后，我们可以定义这个问题了

prob = ODEProblem(f, u_begin, tspan, p)

解决问题

设置完常微分方程后，我们需要得到是 变量 u 与 变量 t 之间的关系，调用 solve 得到这层关系

solve(prob)

这样不够直观，我们绘图看看

plot(sol,
     legend = false,
     linewidth = 2,
     title = "Continuous Compound Interest",
     xaxis = "Time in Year",
     yaxis = "Account Balance in Dollars",
     formatter = :plain,
     widen = true)

ODE 人口增长模型

对于总人口 N 与 时间 t 之间有关系

\frac{dN}{dt} = rN \left( 1 - \frac{N}{K} \right)

其中

• r 表示人口增长率
• K 表示环境可承载的最大人口

我们这样设置函数

f(u, p, t) = p[1]u \left( 1 - \frac{u}{p[2]} \right)

f(u, p, t) = p[1] * u * (1 - (u / p[2]))

我们设置

• N_begin 初始的人口数量为 1.0
• r 每月的增长率为 0.14
• K 最大人口量为 200
• 参数 p 为 [r, K]
• tspan 时间范围 (0.0, 72.0)

然后定义问题

prob = ODEProblem(f, N_begin, tspan, p)

解决他

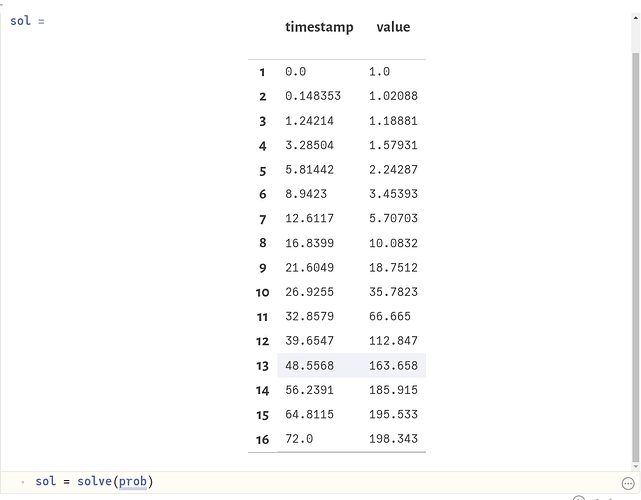
sol = solve(prob)

对其进行绘图

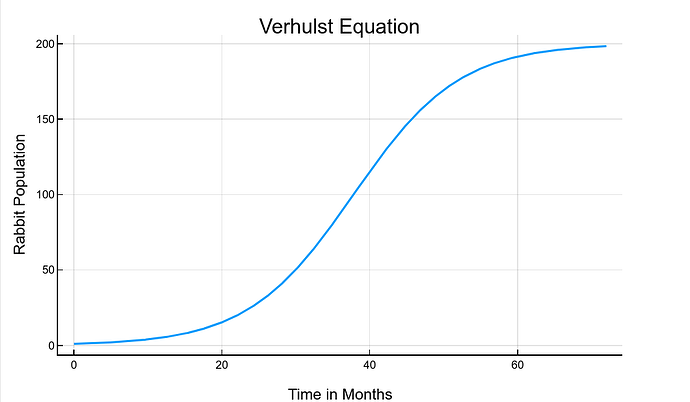
plot(sol,
     legend = false,
     linewidth = 2,
     title = "Verhulst Equation",
     xaxis = "Time in Months",
     yaxis = "Rabbit Population",
     formatter = :plain,
     widen = true,
     xlims = (0.0, 72.0),
     ylims = (0.0, 200.0))

这样我们就得到了总人口 N 与时间 t 的关系

参考

https://www.youtube.com/watch?v=v1l1zmhRuG8&list=PLhQ2JMBcfAsjeC10lx_2zDlFUMkBUTyyO&index=5&ab_channel=doggodotjl
我觉得这个视频作者做的不错，大家可以去点个赞

[nesteiner]

顺带问下大家，这个 Latex 插入的时候该怎么写，我是用 $ 包裹起来的，结果他没有居中
然后我用了 \begin{equation} 结果他没有显示

[RexWzh]

% 两个 $ 居中
$$
\frac{du}{dt} = f(u, p, t)
$$

% 一个 $ 行内
$\frac{du}{dt} = f(u, p, t)$

行内： \frac{du}{dt} = f(u, p, t)
居中：

\frac{du}{dt} = f(u, p, t)