SecondOrder ODEProblem 二阶导数常微分问题
介绍
这里我们探讨下位置u,速度v,和加速度a之间的关系,对于u和v,我们有
\frac{du}{dt} = velocity
而对于v与t,我们有
\frac{dv}{dt} = acceleration
这样,我们得到
\frac{d^2u}{dt^2} = acceleration
我们这样定义函数
\frac{d^2u}{dt^2} = f(du, u, p, t)
描述问题
这里以向上垂直抛出一个小球为例,设向上为y轴,设有函数
f(du, u, p, t) = -g
f(du, u, p, t) = -g
而 g = 9.8067
我们设置
du_begin初始的速度,既向上抛出的速度为 10m/su_begin初始的位置,既抛出时y的位置为 0mtspan时间的间隔为 [0.0, 2.0] 0 - 2 秒之内
这样以后,定义问题为
prob = SecondOrderODEProblem(f, du_begin, u_begin, tspan)
解决问题
sol = solve(prob)
画出他的图像
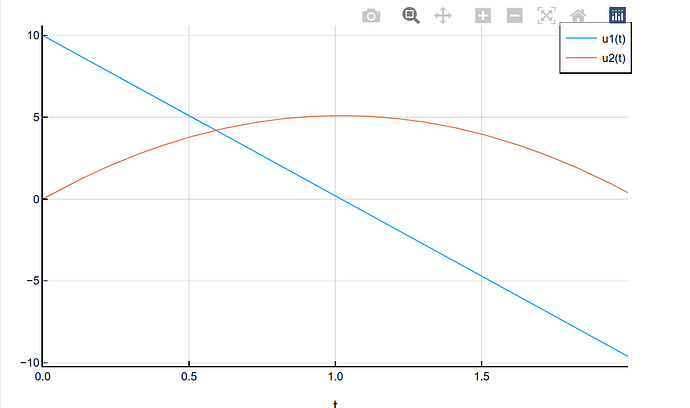
plot(sol)
可以看出,红色的这条线代表位置u,蓝色的这条先代表速度v
SecondOrder ODEProblem 抛球问题
介绍
我们把上面的问题扩展一下,不再是向上垂直抛出小球,而是斜着向上跑出去,看看有什么不同
描述问题
对于位置u与加速度a,他们有关系
\frac{d^2u}{dt^2} = acceleration
我们设置函数f为
\frac{d^2u}{dt^2} = f(du, u, p, t) = [0, -g]
为什么用数组来表示呢,因为他们分别代表两个方向上的加速度,一个是x轴方向的加速度,一个是y轴方向的加速度
那么用数组来代表加速度的话,我们也要用数组来代表速度和位置 ,他们分别代表x轴上的量和y轴上的量
而对于抛出的角度 \theta
\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{vx}{v}
\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{vy}{v}
我们设置
v_begin抛出速度为 100 m/stheta抛出的角度为 \frac{\pi}{4}du_begin抛出的速度向量为[cos(theta) * v_begin, sin(theta) * v_begin]u_begin抛出的位置为[0.0, 0.0]tspan时间间隔为[0.0, 20.0]
这样以后,我们定义问题
prob = SecondOrderODEProblem(f, du_begin, u_begin, tspan)
解决问题
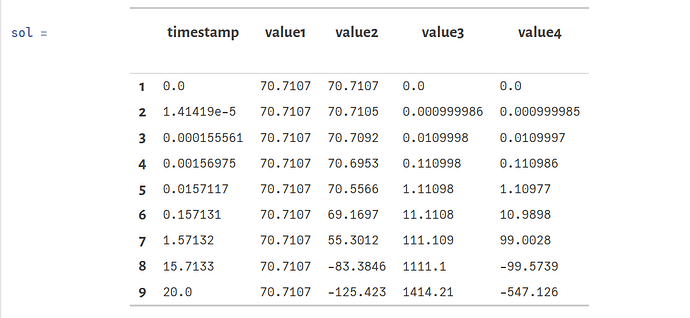
sol = solve(prob)
画出他的图像
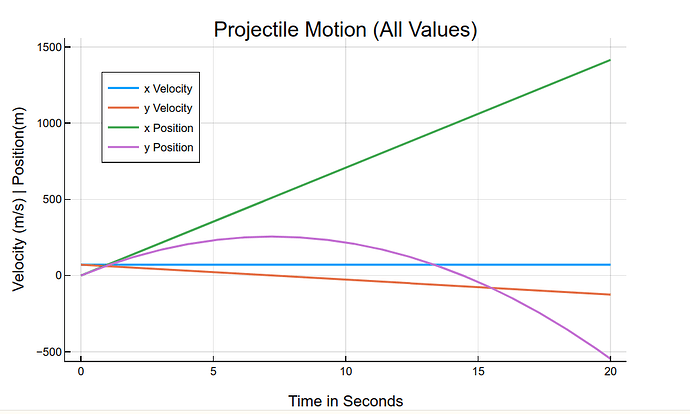
plot(sol,
legend = (0.15, 0.85),
linewidth = 2,
title = "Projectile Motion (All Values)",
xaxis = "Time in Seconds",
yaxis = "Velocity (m/s) | Position(m)",
labels = ["x Velocity" "y Velocity" "x Position" "y Position"],
formatter = :plain,
widen = true,
xlims = (0.0, 20.0),
ylims = (-500.0, 1500.0))