我是一个Julia新手,最近我准备使用DifferentialEquation.jl来求解我遇到的Linbland Master Equation(林布拉德主方程),方程的形式如下:
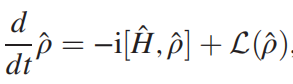
其中ρ是密度矩阵算符,H是哈密顿量,L(ρ)是刘维尔超算符。
正如你所看到的,主方程的变量都是矩阵或者高阶张量。
下面的代码是我网上看到的一段使用DifferentialEquation.jl求解方程的事例:
using DifferentialEquations
using Plots; gr()
f(u,p,t) = 0.98u #新建一个待求方程
u0 = 1.0 #初值
tspan = (0.0,1.0) #时间范围
#新建一个常微分方程问题
prob = ODEProblem(f,u0,tspan)
sol = solve(prob)
#画图
plot(sol)
savefig("ode_1.png")
它计算的是非常简单的一个常微分线性方程,变量都是一个数字。
我的问题是如果我建立一个如下的方程:
LME(rho,t)= -i*(H*rho-rho*H) + L_rho
DifferentialEquation.jl可以正确计算出结果吗?
如果不可以请问Julia中是否有其他库可以解决我的问题,请各位指教。