[DifferentialEquations.jl] ODE 方程组 笔记

[nesteiner]

ODE 方程组问题

介绍

对于变量x,y,t，他们之间有关系

\begin{align} \frac{dx}{dt} &= \alpha x - \beta xy \\ \frac{dy}{dt} &= \delta xy - \gamma y \end{align}

这个时候需要使用 f(du, u, p, t) 形式的函数，其中

• du 代表左边的微分 \frac{dx}{dt} 与 \frac{dy}{dt}
• u 代表 变量的组合， x 与 y
• p 代表常数项

生成这个函数

\begin{equation} f(du, u, p, t) = \begin{cases} du[1] = p[1] u[1] - p[2] u[1] u[2] \\ du[2] = p[4] u[1] u[2] - p[3] u[2] \end{cases} \end{equation}

描述问题

我们以上面的 Lotka Volterra 问题为例
定义Julia函数

function lotka_volterra(du, u, p, t)
        x, y = u
        alpha, beta, gamma, delta = p
        du[1] = alpha * x - beta * x * y
        du[2] = delta * x * y - gamma * y
end

其中

• x 是猎物的数量，比如狒狒
• y 是猎手的数量，比如猎豹
• \frac{dx}{dt} 与 \frac{dy}{dt} 代表两个数量的瞬时增长率
• t 表示时间
• \alpha \beta, \gamma, \delta 描述两个物种相互作用的正实参数

我们设置

• x_begin 初始的狒狒数量为 10
• y_begin 初始的猎豹数量为 10
• u_begin 为 [x_begin, y_begin]
• \alpha 为 0.4
• \beta 为 0.4
• \gamma 为 0.4
• \delta 为 0.1
• tspan 为 (0, 100)
• p 为 [\alpha, \beta, \gamma, \delta]

我们定义问题

prob = ODEProblem(lotka_volterra, u_begin, tspan, p)

解决问题

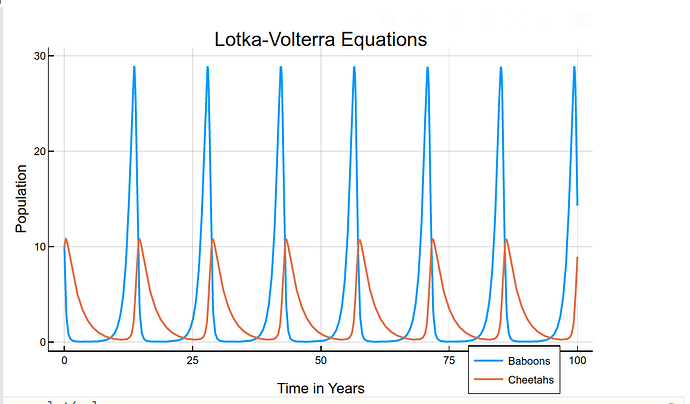
我们要探讨的是x,y对t的关系

sol = solve(prob)

绘制下图像

plot(sol,
     legend = (0.78, 0.09),
     linewidth = 2,
     title = "Lotka-Volterra Equations",
     xaxis = "Time in Years",
     yaxis = "Population",
     labels = ["Baboons" "Cheetahs"],
     formatter = :plain,
     widen = true,
     xlims = (0.0, 100.0),
     ylims = (0.0, 30.0))

ODE 方程组 洛仑兹方程组

描述问题

我们趁热打铁，介绍下洛仑兹方程组
对于变量 x,y,z 对 t 有关系

\begin{align} \frac{dx}{dt} &= \sigma(y - x) \\ \frac{dy}{dt} &= x(\rho - z) - y \\ \frac{dz}{dt} &= xy - \beta z \end{align}

这里我不是专业人员，我也不知道 x,y,z 表示什么，还有剩下的一堆常数，我们按照教程一步一步来
我们设置

• x_begin 为 0
• y_begin 为 1
• z_begin 为 0
• u_begin 为 [x_begin, y_begin, z_begin]
• \sigma 为 10.0
• \rho 为 28.0
• \beta 为 8/3
• p 常数项 [\sigma, \rho, \beta]
• tspan 时间间隔为 (0.0, 100.0)

定义函数

function lorenz(du, u, p, t)
    x, y, z = u
    sigma, rho, beta = p
    du[1] = sigma * (y - x)
    du[2] = x * (rho - z) - y
    du[3] = x * y - beta * z
end

我们定义问题

prob = ODEProblem(lorenz, u_begin, tspan, p)

解决问题

sol = solve(prob, reltol = 1e-8, abstol = 1e-8)

我们需要一些操作，取得 x,y,z 向量(这里是按照教程走的，不用深究)

u = view(sol.u, 1:length(sol.t))
sol_u_matrix = reduce(hcat, u)'
x = sol_u_matrix[:, 1]
y = sol_u_matrix[:, 2]
z = sol_u_matrix[:, 3]

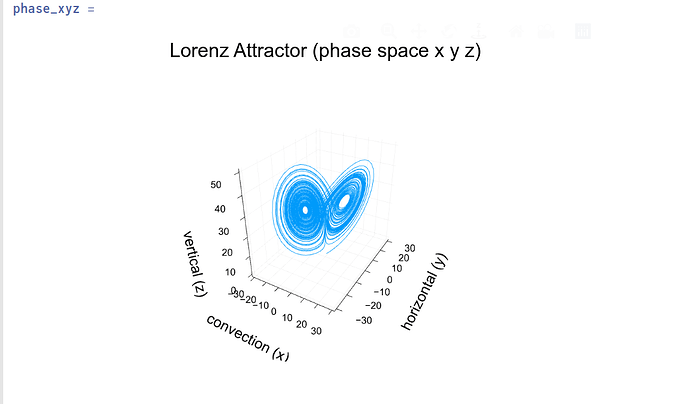
绘制他的图像

plot(x, y, z,
     legend = false,
     title = "Lorenz Attractor (phase space x y z)",
     xaxis = "convection (x)",
     yaxis = "horizontal (y)",
     zaxis = "vertical (z)",
     formatter = :plain,
     widen = true,
     xlims = (-30.0, 30.0),
     ylims = (-30.0, 30.0),
     zlims = (0.0, 50.0))