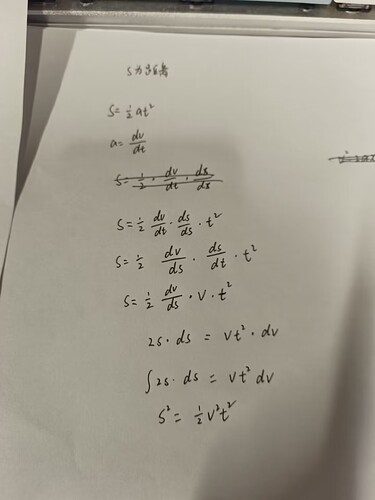[提问] 2023 年第八届数维杯大学生数学建模挑战赛题目B 题怎么做

[nesteiner]

大家好，最近学校给了我们一个作业，要我们尝试解决2023 年第八届数维杯大学生数学建模挑战赛题目，我已经好久没接触过微积分了，有些知识生疏了，需要大家帮帮忙，请帮我看看

---

说明1

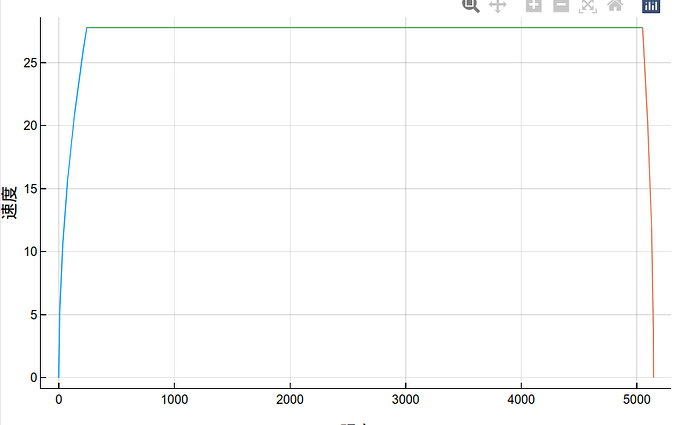
这里 速度与距离 曲线我已经求出来了，我假设牵引力和制动力都是最大，这样方便点，
这是我的代码和曲线

using DifferentialEquations, Plots
using SymbolicNumericIntegration, Symbolics
plotly()

ρ = 1.08
m = 176.3 * 1000 * ρ

s = 5144.7
vmax = 100 / 3.6

R(v) = (2.0895 + 0.0098v + 0.006 * v ^ 2) * 1000
Fmax = 310 * 1000
Bmax = 760 * 1000

# plot s - v
vs1 = range(0, 100 / 3.6, length = 100)
ss1 = map(v -> 1/2 * m * v ^ 2 / (Fmax - R(v)), vs1)
plot(ss1, vs1, legend = false)

vs2 = range(100 / 3.6, 0, length = 100)
ss2 = map(x -> s - x, map(v -> 1/2 * m * v ^ 2 / (Bmax + R(v)), vs2))
plot!(ss2, vs2)

plot!([ss1[end], ss2[1]], [vs1[end], vs2[1]], xlabel = "距离", ylabel = "速度")

这个问题分为三个阶段

1. part1
   加速阶段

牵引力 - f(v) = ma

2. part2
   匀速阶段

牵引力 = f(v)

3. part3
   减速阶段

制动力 + f(v) = ma

问题1

这是我的队友求出来的速度与距离的关系，我不知道对不对，大家帮我看看
第一阶段

s = \frac{\frac{1}{2} m v^2}{牵引力 - f(v)}

第三阶段

s = \frac{\frac{1}{2} m v^2}{制动力 + f(v)}

---

问题2

接下来的问题是如何求出 时间和距离 曲线
我的队友求出来

出来了三个变量 s, v, t ，然后我们就不会做了

[XuJingye]

我不是很清楚旋转质量因数，就知道转动惯量。以下我就忽略旋转相关的东西随便讲讲。

我感觉第一阶段是这样的。无论你利用动能定理 F\Delta s=\Delta\left(\frac{1}{2}mv^2\right)=mv\Delta v ，或者冲量定理 F\Delta t=m\Delta v ，都能得到

[牵引制动力-f(v)]\Delta s = mv\Delta v

这极容易得到：

\frac{ds}{dv}=\dfrac{mv}{牵引制动力-f(v)}

考虑到初始时刻 s(0)=0 ，

s(v) =\int_0^v \frac{mv'}{牵引制动力-f(v')} dv'

第三阶段的话，应该差不多吧，只不过 s(0)=55144.7 m。

---

s = \frac{1}{2} a t^2

是不能用的，它只适合初速度为0的匀加速。你还是回到牛二定律，仿照我上面用微元法解试试吧？核心就是得到微元关系。比如我上面得到纯粹的 s,v,\Delta s,\Delta v 之间的微元关系那一刻，我就觉得成功了——因为你不会求解还可以用程序数值解。

微元关系除了我这样直接得到，还可以联立别的方程，比如结合 s,t,\Delta s,\Delta t 很可能消掉 s,\Delta s 得到 v,t,\Delta v, \Delta t 关系。

用微元法时，还要时刻记得 (\Delta s)^2 和 \Delta s 相比是无穷小，可以忽略。所以你也不用怕微扰展开，或者什么平方操作。

然后你尝试把所有公式列出来，变成方程组，自己解解看吧。

[nesteiner]

额，牵引制动力是什么东西啊

[XuJingye]

牵引制动的合力吧