参数代入方式对函数计算速度的影响

综合讨论区 Julia入门
1

先以一个简单的多项式函数为例来描述我的疑惑

定义一个普通的多项式函数，直接代值计算的速度很快（0.8ns）：

f1(x,y)=x^3*y^3+2*x^2*y+3*x*y^2
@benchmark f1(1.0,2.0)

BenchmarkTools.Trial: 10000 samples with 1000 evaluations.
 Range (min … max):  0.791 ns … 12.333 ns  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     0.875 ns              ┊ GC (median):    0.00%
 Time  (mean ± σ):   0.874 ns ±  0.128 ns  ┊ GC (mean ± σ):  0.00% ± 0.00%

                                        █                     
  ▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▂ ▂
  0.791 ns       Histogram: frequency by time       0.917 ns <

 Memory estimate: 0 bytes, allocs estimate: 0.

但是以参数传递的形式代入，或者提取数组元素代入，均会慢不少（17ns和51ns）：

a = 1.0
b = 2.0
@benchmark f1(a,b)

BenchmarkTools.Trial: 10000 samples with 998 evaluations.
 Range (min … max):  16.366 ns … 36.281 ns  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     17.577 ns              ┊ GC (median):    0.00%
 Time  (mean ± σ):   17.706 ns ±  1.295 ns  ┊ GC (mean ± σ):  0.00% ± 0.00%

   ▃▃▁▃▄▂▅██▅▃                                                ▂
  ▇████████████▇▇▅▅▅▆▆▅▆▄▄▄▄▄▆▅▆██▇▇▄▆▅▄▅▄▃▃▃▁▅▄▄▄▁▃▁▁▃▁▃▁▄▄▃ █
  16.4 ns      Histogram: log(frequency) by time      24.4 ns <

 Memory estimate: 16 bytes, allocs estimate: 1.

c=[1.0,2.0]
@benchmark f1(c[1],c[2])

BenchmarkTools.Trial: 10000 samples with 990 evaluations.
 Range (min … max):  45.833 ns … 202.441 ns  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     49.706 ns               ┊ GC (median):    0.00%
 Time  (mean ± σ):   51.062 ns ±   5.727 ns  ┊ GC (mean ± σ):  0.00% ± 0.00%

           ▁█ ▃▂                                                
  ▄▂▁▁▁▁▁▂▃██▆██▄▃▃▂▃▃▃▃▂▂▂▁▁▁▁▂▂▂▃▂▂▁▁▁▁▁▁▁▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂
  45.8 ns         Histogram: frequency by time         64.1 ns <

 Memory estimate: 48 bytes, allocs estimate: 3.

所以当我想提取一个数组中的数据代入此函数处理，以得到一个新的函数时，新函数的运算速度就会很慢：

arr=[1.0,1.0,1.0,1.0,1.0]

function f2(y)
    res=0.0
    for i=1:5
        res+=f1(arr[i],y)
    end
return res
end    

@benchmark f2(2.0)

BenchmarkTools.Trial: 10000 samples with 362 evaluations.
 Range (min … max):  248.848 ns … 126.508 μs  ┊ GC (min … max): 0.00% … 99.75%
 Time  (median):     266.804 ns               ┊ GC (median):    0.00%
 Time  (mean ± σ):   286.499 ns ±   1.264 μs  ┊ GC (mean ± σ):  4.88% ±  2.70%

       █                                                         
  ▃▄▂▂▂█▅▁▁▃▅█▇▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▃▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂
  249 ns           Histogram: frequency by time          341 ns <

 Memory estimate: 320 bytes, allocs estimate: 20.

可看到循环5次得到新函数的f2，其计算速度为280ns，约为每次代入数组元素值到f1计算时间（51ns）的5倍。

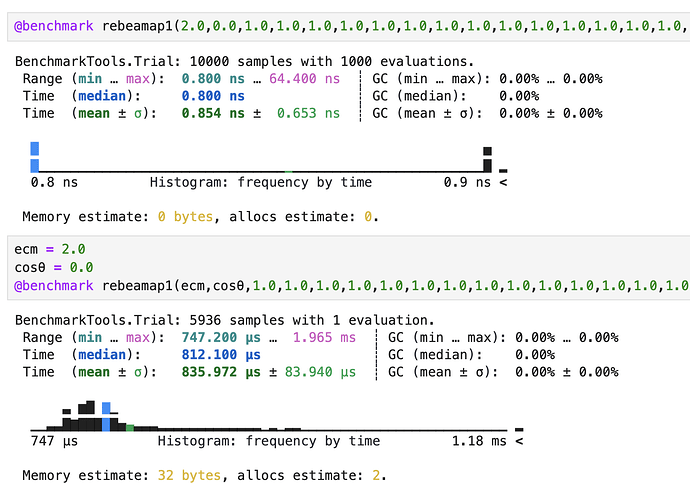
对于上面这个简单函数，几种代参方式速度上的差异可能还不是很大，但当我的函数是一个非常复杂的多项式函数（下图的rebeamap1）时，直接计算 和 传递参数/提取数组元素为参 计算速度的差异十分巨大（从1ns到约700μs）：

image
image1360×954 116 KB

所以当我用其去做例子中的循环提取数组数据，以定义出一个新函数时，速度很不理想。

我的第一个疑问是这种速度差异的主要来源是哪，我猜测可能是函数直接代入常量时会触发编译优化，但是不清楚具体原理以及速度差异为何这么大；
第二个疑问是既然直接代数计算函数的速度很快，是否有优化方法使上面定义f2的例子中，循环中每次提取数组元素的计算，都转换成类似的直接代数计算。还是说这是个原则上没办法实现的事情。

期待大家的解答，万分感谢了！

2

Manual · BenchmarkTools.jl (juliaci.github.io)

1 个赞
3

2楼已经回答了，稍微补充一下。
在@benchmark sum($a)中，$符号用于将a的值插入到表达式中，使其在编译时表现为Julia已知类型的变量。否则，Julia在每次执行基准测试时都要先从全局作用域搜索a，消耗额外的时间。

2 个赞
4

您好，非常感谢您提供的资料！文档里我大概了解到了两件事，不知道是否正确：

  1. @benchmark 的基准测试中，应当将变量以插值方式代入被测函数，这样可以略去对变量的搜索或计算时间，例如：
    a=1 @benchmark f(&a) 等效 @benchamark f(1)，均会比 @benchmark f(a) 省去对a值的搜索时间；
  2. 对于参量全部已知的表达式函数，优化器会将其在编译阶段完成计算，所以此时@benchmark测试的并非真实的计算时间，例如：
    f(x,y)=x+y @benchmark f(1,1) 或者 x=1;y=1; @benchmark(&x,&y) 测试的不是实际f()计算时间，只是简单的返回结果的时间；

所以对于表达式函数，这样的测试结果（0.8ns）可以说是无效的吗：

f1(x,y)=x^3*y^3+2*x^2*y+3*x*y^2
@benchmark f1(1.0,2.0)

BenchmarkTools.Trial: 10000 samples with 1000 evaluations.
 Range (min … max):  0.791 ns … 12.333 ns  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     0.875 ns              ┊ GC (median):    0.00%
 Time  (mean ± σ):   0.874 ns ±  0.128 ns  ┊ GC (mean ± σ):  0.00% ± 0.00%

                                        █                     
  ▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▂ ▂
  0.791 ns       Histogram: frequency by time       0.917 ns <

 Memory estimate: 0 bytes, allocs estimate: 0.

那我该如何测出一个表达式函数的实际计算速度呢？文档里如下的处理方式我测试了一下，好像没有区别（我的计算时间均为1.3ns）：

julia> a = 1; b = 2
2

julia> @btime $a + $b
  0.024 ns (0 allocations: 0 bytes)
3

julia> @btime $(Ref(a))[] + $(Ref(b))[]
  1.277 ns (0 allocations: 0 bytes)
3
5

您好，感谢您的回复！我在下面大致描述了自己的理解，不知道是否正确。速度差距如此之大除了对参量的搜索，是否主要因为参量已知的表达式会在编译中被计算处理，所以测出的不是实际计算时间？